1arey koi toh solve kaor?
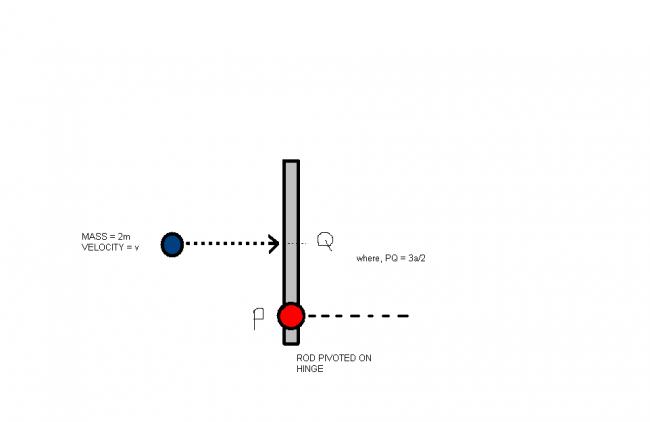
a uniform rod of mass 'm' and length '5a' is free to rotate and hinged at point 'P' point P is at a distance of 'a' from one end.a ball of mass '2m' strikes the rod with velocity 'v' at point 'q'.q is at a distance of '2a' from point 'p'.find the final velocity of ball and angular velocity of rod???
-
UP 0 DOWN 0 0 10
10 Answers
106is it in a vertical plane or horizontal plane.. answers will vary acc to that (if the rod was in a vertical plane then it might have an angular velocity when the particle strikes the rod)
1INITIAL angular momentum L1 = (2m)(2av)=4mav
FINAL angular momentum L2 = (-)4mav"+Iω
...(-) sign indicates that 2m particle rebounds from rod
...here I is about the point P = Icm + m(PQ)2
so..I=13/3ma2
L2=(-)4mav" + 13/3mωa2
since no external torque is acting on the system
INITIAL angular momentum 'L1' = FINAL angular momentum 'L2'
this gives us::
v = (-)v" + (13/12)aω .... (1)
the total energy of the system is conserved...
so...
1/2 (2m) (v2) = 1/2(2m) (v"2) + 1/2 (I) ω2
=>
v2 = v"2 + (13/6) (aω)2 .... (2)
solving the 2 equations we get :
final velocity of the ball = v" = (11/15)v
angular velocity of the rod about P = ω = 8v5a
1i know the answer is wrong :P ... plz n e one help me ..!!! :'(
23let J = impulse due to collision
J = 2m(v2m+v) ...(1)
now hinge also applies force on the rod , so to refrain frm involving it ,
write the eqn for angular impulse of J abt P
J (2a) = Ipw = m ( 52a2
12 ) w
so J = 13maw6....(2)
vm= cel of com of rod = 3aw2 .....(3)
e = coeff of restitution
vq=2aw
e =2aw +v2m v ...(4)
unknowns - J,vm , v2m, e , w i.e 5 unknowns , 4 eqns
if e = 1 , problem is killed
49without knowing whether it is perfectly elastic/inelastic and if it is partly inelastic then without knowing the value of e at least i cannot think of a solution yet!
i think it should be given!
1sorry for error i found the same qestion in other books.....there it is given tht e=1/4..
sorry to all who showed their interest in it
and i gt the anwser
by simpl conserving angularmomentum..and using equation of e.