23vA1 = v/2 ??
vA2=5v/6 ?
vB2 = -v/6 ???
Traditionally been weak in this part of mechanics...pulley problems samajh aate they magar usse zyaada nahi.
Q. A hinged construction consists of three rhombuses with the ratio of sides 3:2:1 . Vertex A3 moves in the horizontal direction at a velocity v. Determine the velocities of vertices A1, A2, and B2 at the instant when the angles of the construction are 90 degrees.
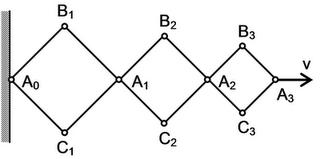
How am I supposed to approach this? Kisi cheez ko constant lena hai...magar kisko?
-
UP 0 DOWN 0 0 7
7 Answers
39I asked for the approach yaar...I don't have the answers.
23take B3A3 = r , B2A2=2r , B1A1=3r
now take angle B1A1A0 = B2A2A1=B3A3A2= a
vA1 = d(A0A1)/dt = d/dt ( 2 x 3rcosa)
now
\frac{d(A_{1}A_{2})}{dt} = v_{A_{2}}-v_{A_{1}}
so v_{A_{2}}= \frac{d(A_{1}A_{2})}{dt}+ v_{A_{1}}
v_{A_{2}}= \frac{d(2\times 2rcosa)}{dt}+ v_{A_{1}}
\frac{d(A_{2}A_{3})}{dt} = v_{A_{3}}-v_{A_{2}} = v-v_{A_{2}}
v=\frac{d(A_{2}A_{3})}{dt}+v_{A_{2}}
v_{B}=\frac{d(2rsina)}{dt}
now find relation between v ,r , da/dt .
39Nice! It sort of makes sense now :D
You took A0 as your stationary reference point and measured everything from there. To find the bases of those triangles you used trigo in a half triangle then multiplied by 2.
To find the velocity of A1 you again used A0 as a reference point, by subtracting those specific velocities. Nice one!
