DOUBT IN ROTATION.

is the asnwer

= ω²2α*2Ï€ where α= 5gk(k+1)2R(k²+1)

please verify

ANS. IS (1+K²)w_o²R8pik(k+1)g

w is actually omega..

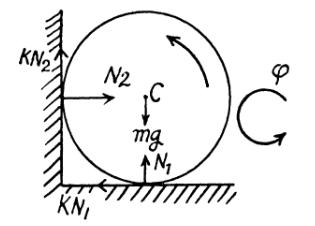
So by balancing the forces we get
N₁ + kN₂ = Mg
N₂ = kN₁

N₁ + k²N₁ = Mg
(k² + 1) N₁ = Mg ..........................1

by balancing the torque abt the centre of cylinder we get..
(kN₁ + kN₂ ) = MR² α / 2
k(N₁ + kN₁) = MRα/2
k(k+1)Mg / (k² + 1) = MRα/2 from 1

So α = 2k(k+1)g / (k² + 1)R
Now 0 = ω + αt
so t = -ω/α

Now θ = 1/2αt²
= 1/2 α * ω² / α²
= 1/2 ω² / α

= ω²(k² +1)R / 4k(k+1)g..
Now number of turns = θ / 2πR....
: )