21thnks got it.
a small heavy block is attached to the lower end of a light rod of length l which can be rotated about its clamped upper end.what minimum horizontal velocity should be given so that it moves in a complete circle?
-
UP 0 DOWN 0 0 5
5 Answers
21the answer given is 2√gl but i think it should be √5gl. pls help which is right?(hcverma-1 pg-135 q.49)
4It is √5gl for a string and not rod
In the qs a rod is given
So ans is 2√gl
19n.b.....you are getting that answer because you are supposing that a string and a light rod are the same !! there is a subtle difference between the two !
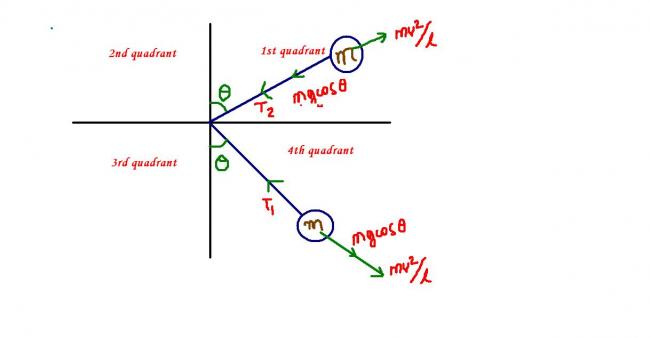
when the mass is at any pt in the 4th quadrant
T1 = mg cosθ +mv1 2/l
when the mass is at any pt in the 1st quadrant
T2 = mv2 2/l - mg cosθ......(suppose the two angles are equal,,,can be different also)
T1 cannot be zero as it is an addition of 2 positive quantities, but v1 can be zero. when v1 becomes zero, the body stops and comes back again ! thus the 4th quadrant cn become a zone of oscillation !
on the other hand v2 cannot be zero as that would make T2= 0 at some point, which is impossible because a string cannot take compression ! thus velocity cannot be zero but tension can be zero in the 1st quadrant ! when T2 becomes 0 , c.p. force ceases to act and circular motion stops,,the body now follows projectile motion !
but when we use a massless rod, the velocity can become zero in the 1st quadrant.
applying conservation of energy theorem ,
1/2 mv12 = mg(2l) + 1/2 mv22
....putting v2 = 0 for light massless rod, we get v1=2√gl
1there is no tension at rod. so P.E at highest point is equal to K.E at lowest point .
since length of rod is l.therefore distance betn lowest & highest points is 2l
mg(2l)=1/2mv2 ,v=velocity at lowest point
v=2√(gl)