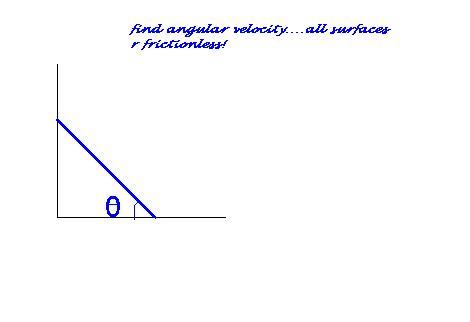
@euree point out mistake in above solution y i m not getting same answer as you!!!!!!
5 Answers
hacker
·2010-02-09 23:13:19
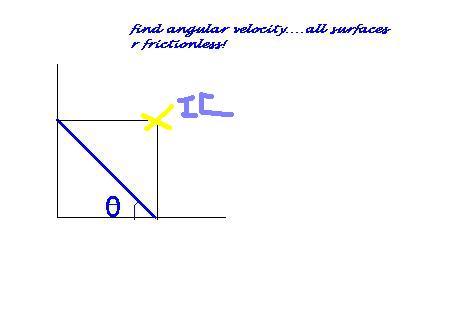
as friction is absent!\so,
mgl/2[1-sin@]=1/2I(ic)w2
I(ic)=ml2/12+ml2cot2@/4
>w=√12g(1-sin@)/l(1+3cot2@)
hacker
·2010-02-09 23:13:54
rahul nair
·2010-02-10 03:20:26
u have neglected the Normal reactions exerted by the wall an the ground on the rod......
hacker
·2010-02-10 03:55:07
@rahul[i think u can see i have considered earth and rod as a system so i don't think that error is coz of normal reaction[3][3]]
plz post ur solution!
rahul nair
·2010-02-10 05:08:29
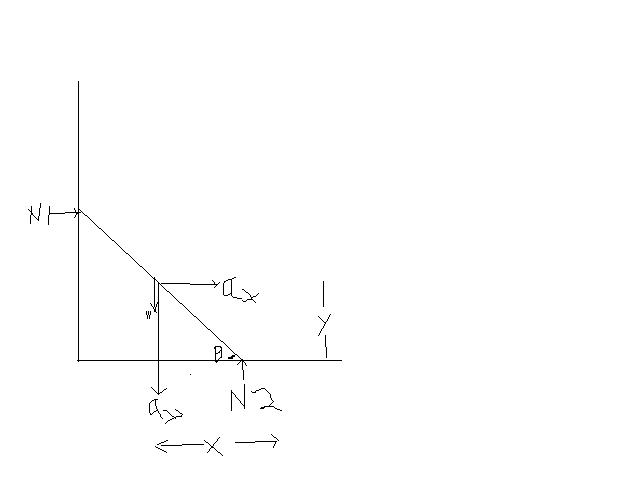
Eqns for com of rod:
(ax & ay are horizontal & vertical component of acc. respectively)
1.N1=max
2.N2-mg=may
Torque abt COM
3.
(N2cos@-N1sin@)l/2=ml\alpha2/12
x=lcos@/2, y=lsin@/2
Diff. twice
4.ax=l(\alphacos@-w2sin@)/2
5.ay=-l(\alphacos@+w2sin@)/2
solving these eqns,\alpha=3gcos@/2l
&use \alpha=w(dw/d\theta)
so w=√3g(1-sin@)/l