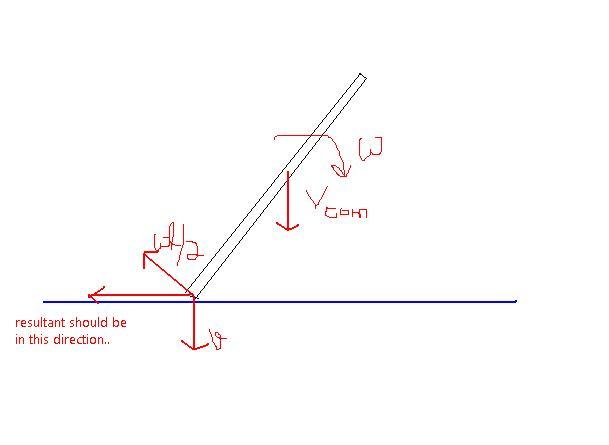
also by instantaeneous center method v=wl/4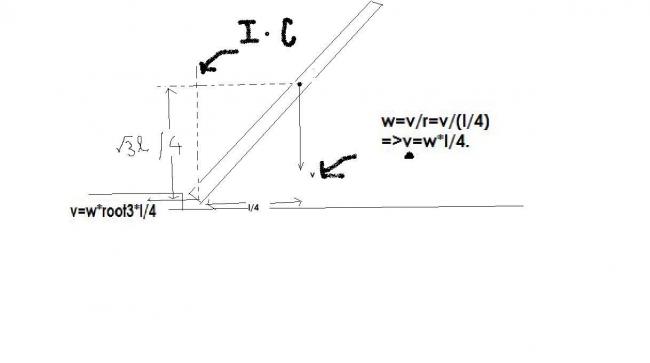
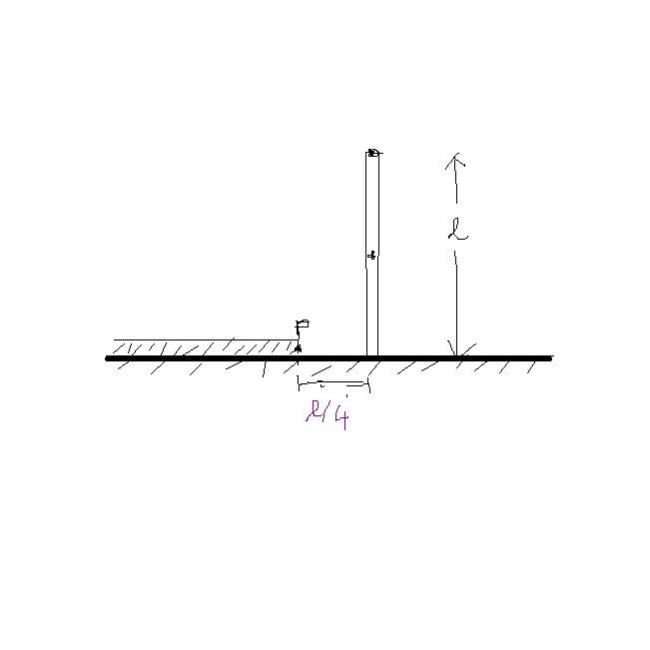
passage: a rod of mass m n length l is placed vertiaclly on a smooth floor as shown in the fig.. The lower end of the rod is given a negligible slight push towrds left due to which the lower end of the rod moves towards left and collides perfectly inelasticaly with the fixed point P and the rod rotates about the point P. [ l = (2 - √3)m ]
1.) the angular vel of the rod just before its lowest point collide with P is --
a) √48g/13
b) √24g/7
c) √21g/7
d) √20g/13
u can chcek the ans if u get anything...
ans ->ans: b
-
UP 0 DOWN 0 0 17

17 Answers
Vcom=ωl/4 ....(because velocity of lowest point is only along plane..) ----> din get [2] [2] [2] [2]
post added to above (post 9... designer post :P) to complete the soln
now is it clear...
ωl/2cos600=v
v=wl/4..
hey am sry 4 not understanding :P but for last two i have been constantly finding out wrong ans ... n am fedup wid my rusted mind [2]
cant we conserve angular momentum about point P???
mvl/2 = Ipw ??
plz correct if wrong...
2.) the angular velocity of the rod just afetr its lowest point collides with P is :
a) g/4
b) g/2
c) √21g/8
d) √21g/32
â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹
Vcom=ωl/4 ....(because velocity of lowest point is only along plane..)
mgl/4(2-√3)=1/2mvcom2+1/2ml2/12ω2...
Put vcom and value of l to get answer√24g/7..
[1]
__________
added later to complete the soln..
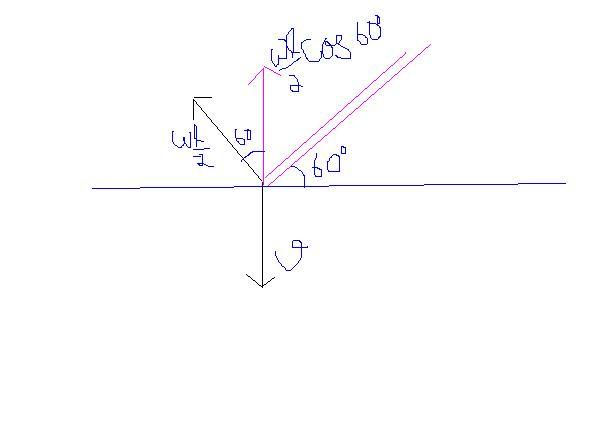
now is it clear...
ωl/2cos600=v
v=wl/4..
â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—â—‹â—