Fluid doubt................

hey abhishek...

i will give u a hint...

Pressure is equal in all directions...

multiply pressure by the elemetary cross section to find elementary force... take the horizontal componont! vertical component u can assume will be neglected *though it will be small! *because of the height of the tube)

Before that u need to find the pressure at each component...

so that can be done by bernaulli's equation..

I think this hint enuf.. if u are still unable to solve.. u will get the solution..

This question has briliant funda.. but unfortunately not so brilliant proof.. had the solution been a bit simpler it would have been one of the classic problems...

V_r=v = √2gh

using continuity equation,

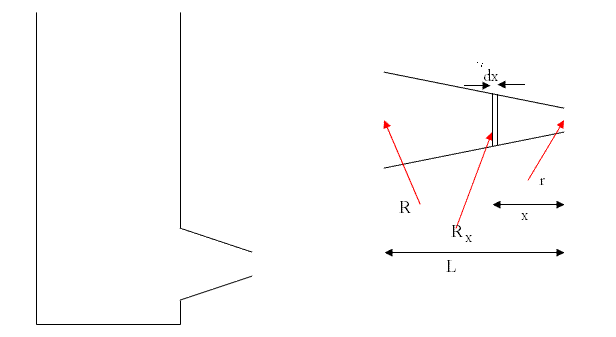
V_R.(Area at L)=V_x.(Area at x)=V_r.(Area at 0)

Also, force will be normal to the tube.

So for the band of section dx, the net force in the forward direction will be

pressure at that point × area × sin θ

Now, we also have bernaulli's equation with us.

So we have to find Pressure at that point using bernaulli;s prinicple.!

θ is found by (R-r)/L

Obviously R, r are found by the respective areas given in the question.

Note that on the tube, atmosphere will be applying a pressure P₀ in the inward direction.

So the net pressure will be P-P₀

So when finding force, it will be integral over pressure × area where pressure will be the pressure difference wrt to atmospheric pressure.

This force F will be

∫(P-P₀)2.pi.R_x.dx. sinθ

limit of integral is from 0 to L

R_x=r+(R-r)/L.x

height can be considered same thoughout the tube. THis is cos the tube is very thin wrt the height of the whole container.

We know the the velocity at the outlet is √(2gh)

Apply bernaulli's principle within the tube.

we get P_x+ρgH+1/2ρV_x²=P₀+ρgH+ρV₀²

so P_x-P₀=1/2ρ(V₀²-V_x²)

now what remains is to integrate...

first we need to substitude Vx using the continuity equation as well !