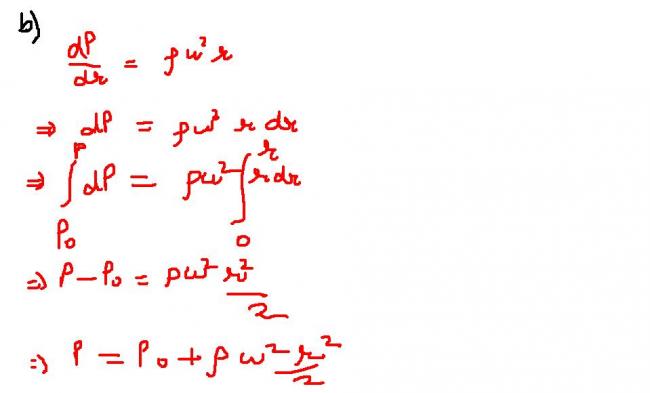i htnk it was done by sharman some time back..
Q1. A cylindrical container of an incompressible liquid with density Ï rotates with constant angular speed ω about its axis of symmetry, which we take to be the y-axis. (a) Show that the pressure at a given height within the fluid increases in the radial direction (outward from the axis of rotation) according to ∂p/∂r = Ïω2r. (b) Integrate this partial differential equation to find the pressure as a function of distance from the axis of rotation along a horizontal line y=0. (c) Show that the surface of the liquid has a parabolic shape i.e. the height of the liquid is given by h(r) = ω2r2/2g.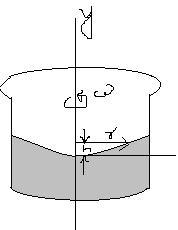
Please explain the answer with suitable diagram.
For part (c) will P=Po+Ïgh be applicable?
-
UP 0 DOWN 0 0 11

11 Answers
Q2. An incompressible fluid with density Ï is in a horizontal test tube of inner cross-sectional area A. The test tube spins in a horizontal circle in an ultracentrifuge at an angular speed ω. Gravitational forces are negligible. Consider a volume element of the fluid of area A and thickness dr' at a distance r' from the rotation axis. The pressure on its inner surface is p and outer surface is p+dp.
(a) Show that dp=Ïω2r'dr'.
(b) If the surface of the fluid is at a radius ro where the pressure is po, show that the pressure p at a distance r≥ro is p=po+Ïω2(r2-ro2)/2.
(c) An object of volume V and density Ïob has its centre of mass at a distance Rcmob from the axis. Show that the net horizontal force on the object is ÏVω2Rcm, where Rcm is the distance from the axis to the center of mass of the displaced fluid.
(d) Explain why the object will move inward if ÏRcm>ÏobRcmob and outward if ÏRcm<ÏobRcmob.
(e) For small objects of uniform density, Rcm = Rcmob. What happens to a mixture of small objects of this kind with different densities in an unltracentrifuge?
Please give a diagram along with answer as well. I cudnt do this quesn bcz cudnt understand the diag.
Q1
i have done simple derivative...u can take it as partial derivative..it wont have an effect on overall eqn[1]
assume a tube and take an elment dr at distance r from axis
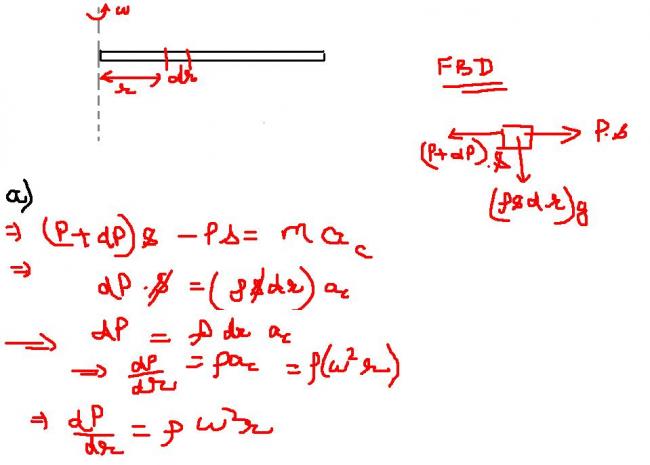

in the end i typed y=ω2x2/2Ïg
but it is y=ω2x2/2g
sorry for the mistake[1]
Eure for Q2.
i cant understand what Rcm, Rcmob are and the meaning of the last two bits
a new body (red) of volume V is inserted...
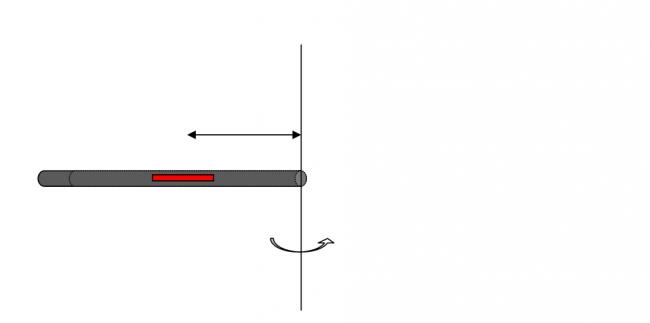
Now is the question more clear?
yes sir i was able to solve the first two bits.. but then Rcm, Rcmob .. i cudnt understand their meanings and positions ...
The black line (arrow drawn in the second image of #10 gives Rcmob
Rcm is the distance of the CM of the displaced liquid..