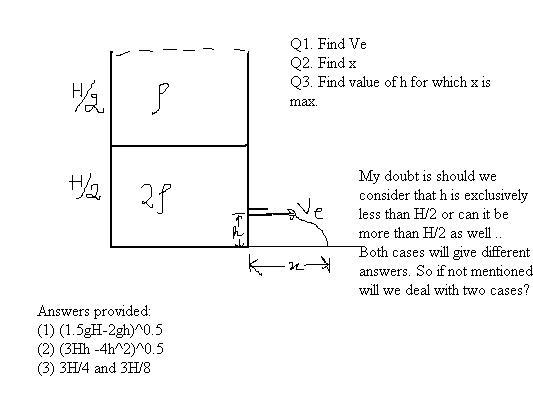
106sir, even if we consider h < H/2 and h > H/2 for (3) I am not getting 3H/4 ..
6 Answers
1357yeah consider it less that H/2 as shown in the figure, for Q1 and Q2
106
24Ans1
v_e=\sqrt{\frac{2g[(\rho \frac{H}{2})+2\rho (\frac{H}{2}-h)]}{2 \rho}}
24Ans2
-h=-\frac{gt^2}{2}=>t=\sqrt{\frac{2h}{g}}
and x=v_et
=> x=\sqrt{3Hh-4h^2}
24v_e=\sqrt{\frac{2g[(\rho \frac{H}{2})+2\rho (\frac{H}{2}-y)]}{2 \rho}} ;t=\sqrt{\frac{2y}{g}};x=v_e.t
For xmax
\frac{dx}{dy}=0
1357For third one I think there will be only one answer
both the answer are incorrect
the answer I m getting is h=H/2+0