Mechanics - fluids revision

24

eureka123 ·2009-02-25 02:40:58

Q2 ka ans kya hai??

UP 0 DOWN 0
Post on FacebookPost anonymously?

3

iitimcomin ·2009-02-25 01:41:55

sorry for delayed response i didnt see ur question before[2][2][2]

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-25 01:43:28

ok thanx pls try 2nd question.

UP 0 DOWN 0
Post on FacebookPost anonymously?

3

iitimcomin ·2009-02-25 01:44:49

sorry yaar if m0 is given only and not h then u can rite AÏH = M0 .....

so ull get height in terms of given variables for the second Q (of Q1)solution above!!!!!!!!!!!!!

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-25 01:47:41

ya i know..... plz try 2nd question..

UP 0 DOWN 0
Post on FacebookPost anonymously?

3

iitimcomin ·2009-02-25 01:47:43

Q2 minimum ya maximum???????

UP 0 DOWN 0
Post on FacebookPost anonymously?

3

iitimcomin ·2009-02-25 01:55:17

ÏƒgLÎ R² = mg + ÏgLÎ R² ......

ÏƒLÎ R² - ÏLÎ R²= m ............

LÎ R²(Ïƒ-Ï) = m ..........................

this is maximum value!!!!!!!!!!

u want minimum ya maximum?????

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-25 01:56:23

even i now maxm value.... but its asking minm.... [2]

UP 0 DOWN 0
Post on FacebookPost anonymously?

3

iitimcomin ·2009-02-25 01:58:24

@eureka ur approach and ans. for accn. are rite but ur way dosnt justify that a is a constant with time which is req. for the second part ........... just my view [1]

UP 0 DOWN 0
Post on FacebookPost anonymously?

3

iitimcomin ·2009-02-25 02:04:43

MINIMUM VALUE DEPENDS...........IF Ïƒ/Ï<=1 ITS 0!!!!!!!!!!!!!!

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-25 02:06:13

given in question that Ïƒ>Ï

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

vector ·2009-02-25 02:37:59

asish(1) balance d force of gravity n buoyant force (2)apply centre of gravity s y coordinate above centre of mass coordinate solving u ll get d ans i think
did u try it???/

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-24 22:08:41

koi to solve karo ise...

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

vector ·2009-02-25 02:43:07

@eureka ve u got d ans???

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-25 02:53:54

answer hai Î R²L(√ÏÏƒ-Ï)

UP 0 DOWN 0
Post on FacebookPost anonymously?

33

Abhishek Priyam ·2009-02-25 03:55:29

din saw...
:P

koi nahi banaya.. :O

dekhte hain....

UP 0 DOWN 0
Post on FacebookPost anonymously?

33

Abhishek Priyam ·2009-02-25 04:38:32

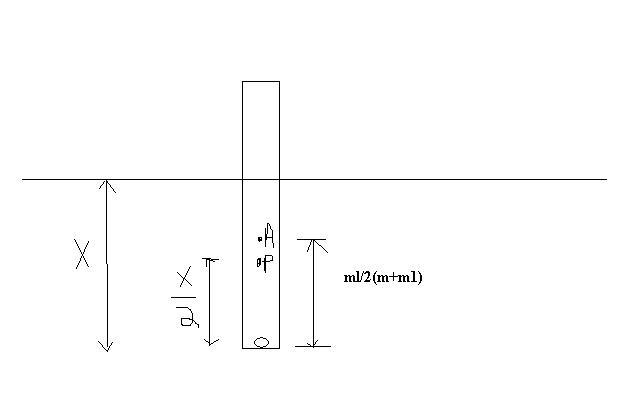
(in the fig right side it is.. mL
2(m+m₁)

No for stable equilibrium P should be above A..

x/2â‰¥ml/2(m+m₁).. (i)

m is mass of rod.. m₁ is mass of point mass..

also xAÏƒg=(m+m₁)g

x=(m+m₁)/AÏƒ

from (i) for minimum m₁..

x=ml/(m+m₁)

(m+m₁) = ml/(m+m₁)
AÏƒ

(m+m₁)=√mlAÏƒ

m=AlÏ

m₁=lA(√ÏÏƒ-Ï)
A=Ï€R²

so m₁=LÏ€R²(√ÏÏƒ-Ï).. ans

UP 0 DOWN 0
Post on FacebookPost anonymously?

3

iitimcomin ·2009-02-25 04:46:50

nice 1 priyam!!!!!!!!![1]

UP 0 DOWN 0
Post on FacebookPost anonymously?

33

Abhishek Priyam ·2009-02-25 05:40:37

[1][2] par pink kyun nahi hota mera.. :(

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-25 08:40:41

bhaiyya priyam ka solution pink kyon nahin hua?

UP 0 DOWN 0
Post on FacebookPost anonymously?

33

Abhishek Priyam ·2009-02-25 08:43:19

sayad tumhara confirmation ka intzaar tha... :)

ab kar denge sayad..

UP 0 DOWN 0
Post on FacebookPost anonymously?

24

eureka123 ·2009-02-25 08:51:23

becoz of ur reply...i am bookmarking it.................gr88 work priyam.....

UP 0 DOWN 0
Post on FacebookPost anonymously?

33

Abhishek Priyam ·2009-02-25 08:53:19

;)

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-24 09:07:15

wat abt (ii) part? and Q2.?

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-24 08:36:46

find answer..... (s) both of them

UP 0 DOWN 0
Post on FacebookPost anonymously?

106

Asish Mahapatra ·2009-02-24 08:41:48

Q2. A wooden stick of length L, radius R and density Ï has a small piece of metal of mass m (of negligible volume) attached to its one end. Find the minimum value for the mass m (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density Ïƒ (>Ï)