This is another problem from an online contest... (This is another of the unsolved problems.. which if not solve.. you should definitely give a good thought)
Prague Physics Challenge, 2nd round
Falling pen
Imagine that you are in your classroom during some very boring lecture. You have nothing to do, so you play with your pen or pencil. Suddenly, the pen gets out of control and falls freely on the corner of the table you are sitting at. You dropped your pen so luckily that it doesn’t spin; it just falls, preserving the angle
between the pen and the desk of the table. The angle between the pen and the edge of the table is 90 degree (so the problem is 2-dimensional). You can suppose that the pen is just a 1-dimensional segment with mass m, length l, and constant linear density m/L. The situation in the moment when the pen touches the corner of the table is shown in the figure 1.
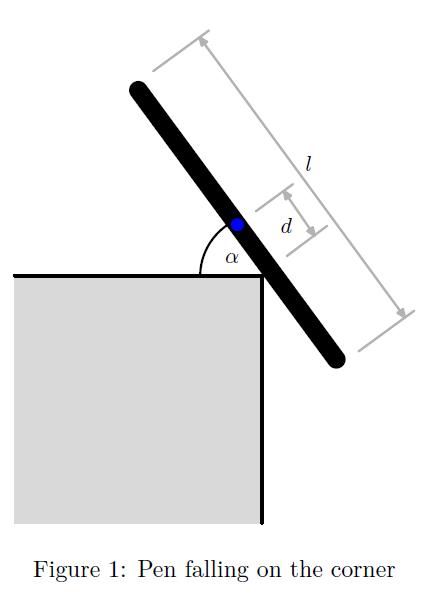
The velocity of the pen in this moment is v0 and its direction is completely vertical. The distance
between the point of touch and the centre of mass of the pen (blue dot in the figure 1) is d. Suppose that there’s no friction between the pen and the corner and all interactions are completely inelastic.
1) establish any kind of equations of motion describing the movement of the pen after it starts touching the corner and before it leaves the corner completely and continues its journey to the floor (it may be necessary to discuss several possible situations – for example, in the case d = l
2 ,
= 0, the pen will just fall onto the the table and will lie there before you pick it and try it again),
2) try to find as general solution of these equations as possible; if you won’t find any solution
in closed form, try to solve the problem numerically,
3) try to find the velocity and the angular velocity of the pen after it stops touching the
corner. Is it possible for the pen to move upwards in this moment?
Original link: http://ppch.eu/sets/2009_2/pen.pdf
-
UP 0 DOWN 0 1 0
