1is the answer F=2(mu)mg
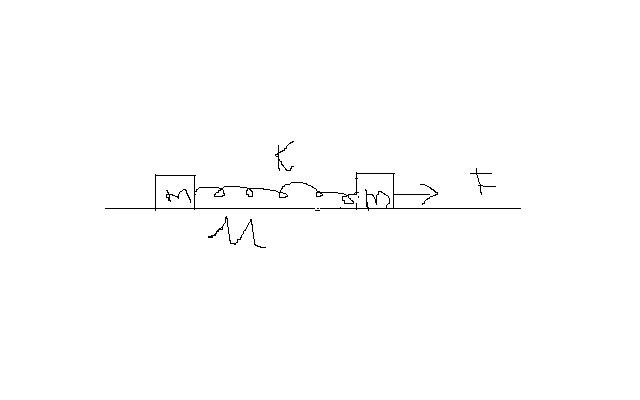
TWO BLOCKS ARE CONNECTED BY A SPRING.THE BLOCKS R PLACED ON A ROUGH HORIZONTAL SURFACE.BOTH R OF EQUAL MASS, WITH CO-EFFICIENT OF FRICTION AS mu BETWEEN BLOCK AND SURFACE.
MINIMUM HORIZONTAL FORCE ON ONE MASS SO AS TO MOVE ANOTHER IS/?
-
UP 0 DOWN 0 0 14
14 Answers
1net force on the right block = F - (umg + kx)
let the maximum extension of spring till the left block remains undisplaced be x0.
so, kx0=umg....
x0=umgk
now since the KE of the left block before moving and the right block before moving is 0, change in KE = 0
so work done = 0
so now integrating [F-(umg+kx)]dx from 0 to x0,
we get, work done = Fx0 - umgx0 - kx02/2 = 0
so from here,
F=umg+kxo2
=umg+umg2
= 3umg2
1for the 2nd body
T-f=Ma
.. for the 1st body
Ma=F-(T+f)
solving these two we get ..
2T=F
Now, if this force is just sufficient to move the 2nd body,
then on considering this limiting case(F->0 r.h.limit)
we get F=T-f (F->0)
so,we get T=f=uMg
since F=2T
therefore F=2f=2uMg
1abhi plz don't involve kinetic energy here,because a non ideal ,friction surface is involved ,due to which there is loss of energy in the form of heat ,that we cannot account for....always make a simple eqn and then examine limiting cases for such qns
1even lower force ..when we start pulling with a compressed spring :)
106abhi's answer is correct . (similar irodov question also there)
1even i hv the same doubt as prateek....how could u ignore work done by friction here
1yup!abhirup!!!!but tht day i thought u did not solve the question correctly as u did not reply when i asked u where u got tht zero from.......i know i was obviously doubting a genius but still i wanted to ensure tht u work-energy theorem or just just got tht zero by chance :P :P :P
1why is the role of friction ignored here .. :'( plz n e one help