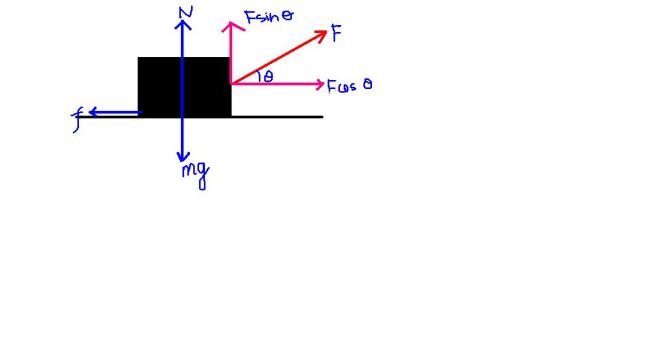
let f= limiting frictional force=μmg
if F is applied parallel to the ground, then it is quite obvious that F≥μmg for the block to move
if F is aplied at an angle θ to the horizontal, then we draw the FBD and balancing the horizontal and vertical components we get
N= mg - F sinθ and
F=( μmg)/cos θ +μsin θ......for the condition when the external applied force just overcomes limiting fric force!
for min F , den must be max,,,,after suitable maximizations and minimizations , we get FMIN =(μmg)/√(μ2+1)
that is the answer !! job done !