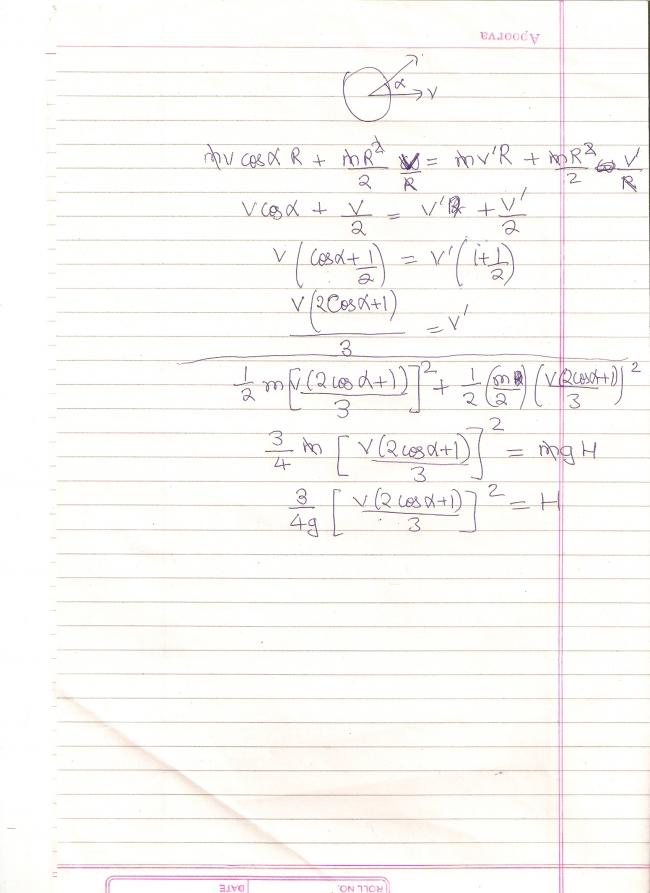
im gonna keep posting some good problems in mechanics from now on. u wudnt find these problems to be really fundu. level or or sumthing, but wud still find it conceptual enuff.some rules u have to follow while doing this will be that u either solve the problems, or post hints, but plz dont give links to any such problem solved earlier. all u jee 2010 aspirants are most welcome to attempt these problems.
1)find the time period of the following set-up
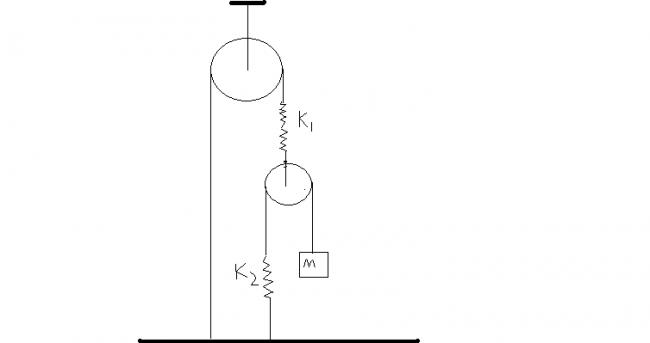
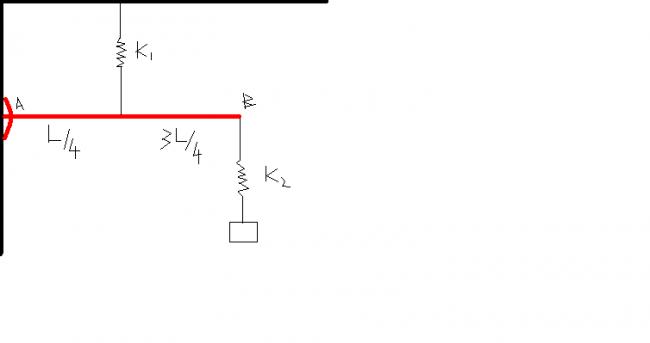
2)find the time period of the following set up.(rod AB is massless)
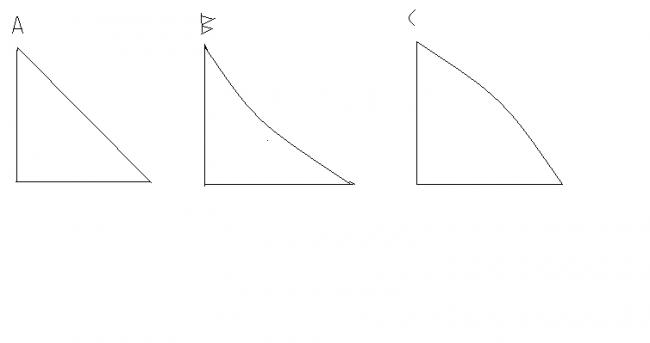
3) a mass 'm' (particle mass) is left free at the top of 3 different paths A), B) and C), thru' which path wud it have maximum KE when it reaches down, given that the coeff. of kinetic friction in all the 3 paths is 'K'
solve these many for now, ill be back with some other prob.s
cheers!!
-
UP 0 DOWN 0 5 40

40 Answers
iitimcomin, i think ans 5) is okay,
in q.4) i think u have commited 2 mistakes, 1 silly mistake and 1 proly a more conceptual mistake.
in line 1 of #27,
when u say (MR2+mR2), that shud be (MR2+mK2R2) moment of inertia..
in second line when u say (alpha)*R =a,
it shud be (alpha)*r=a where r is the distance of centre of mass from the centre of the disc., otherwise, ur solution should be perfect.
tell if any problem.
cheers!!
iitimcoming, perfect answers for 1) and 2), atleast match with my answers if not 100% correct good work.
try these:
4) there is a disc of mass 'M', placed on the floor. (smooth) , the disc has got a mass 'm' at a distance 'Kr" where 'r' is the radius of the disc.
a)find the instantanious normal force experienced by the disc system.
b) instantanous accn. of the mass 'm'.

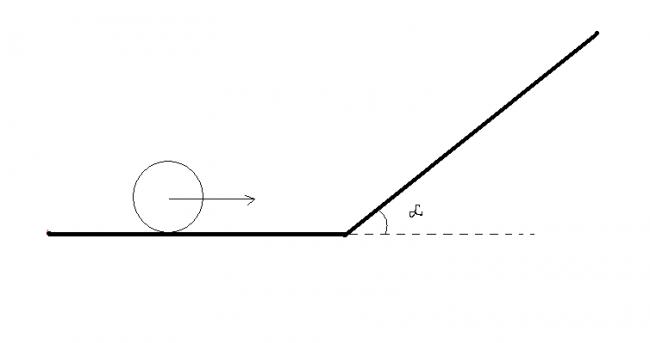
5) a disc of mass 'm' is pure-rolling at a speed 'v', it encounters an
inclined place, of angle 'alpha', the plane being rough enuff to ensure pure rolling of the disc. to what height does the disc rise up?
try them out.
asish, 1 question, can we conserve energy here?
does the disc suffer an elastic or inelast. collision at the instant it
climbs up the incline?? if it was elastic, what happened to the
component of vel. of the disc perpendicular to the plane
mgKR = (MR2/2 + mk2R2)[ALPHA] ........
mgk = (M/2+k2m)R α
mgk2/ (M/2+k2m) = accn ......
good work iitimcoming,that was exactly what i was expecting... i think u remember the q. where we dropped a disc from a hight on an inclined plane :), exactly the similar concept.
for those who didnt understand the problem no. 4),
there is a disc of mass M and radius 'R'. there is a small mass 'm' attached to the disc at a distance 'KR' on a smooth floor. find the instantanous Normal force on the disc from the ground.
let k1 elongate by x1 and k2 by x2 ...
2T = k1x1
T = k2x2 !!!!
x = 2x1 + x2 .....
x = 4T/K1 + T/K2
K1K2/m[4K2 + K1] = w^2 ....!!!!!!!!!
cn take it frm here ...
yep.. the first 1 was silly .. and the second 1 i left r in the same side if u noticed ie i grped a*r
@gordo : time due for more questions ??
not trying to pester you or anything just thought maybe you forgot about this thread [1]
Okay, if Gordo is nowhere around, I'll try to fill in the gap:
To start with a simple problem:
A rope ladder with a length L carrying a man of mass m at its end is attached to the basket
of a balloon with a mass M. The entire system is in equilibrium in the air. Find the work the man should do to climb into the basket. Justify.
rapidfiresh guess :
mgMLM+m or is there something more...
this should be the work done on the man ?
ok [12]
maybe m2M+mgL
I have assumed that the climb is one with no acceleration ?
oh i have a bad feeling about all this......
I am sleeping ... :(
iit comin ur wrong abvt that sum of rods the inertia of rod isnt 0 ur missing inertia ml^2
plz post solution and can u write it more clearly?
i dont know what the answer as i made it up
for the third is it a)
1 and 2 can be solved by finding the total energy of the system and we know dat total energy is constant so differentiating the total energy we will get the ang. frequency
for the third the k.e at the end of the path is the same in all the cases:
reasons:
(1) work done is path independent and is hence the same in all three cases.
(change in p.e. is same in all the cases.
........hence the change in k.e. is also the same in all cases!!!
this is just a try!!!!! may be correct or wrong!!!!
....for the first one its quite simple.....steps are:
(1) total elongation=total contraction
(2) conserve energy and then differentiate
(3) get the answer!
In the 2nd problem, rod AB can be replaced by an equivalent spring (keeping torque const.), I guess, that's the key....
@msp and @organic, did u guys see that the coeff. of friction in all case is non zero. plz try again. ur arguement assumes that work done by friction in all 3 cases is the same. which isnt the truth., so plz recheck.
@organic, are u very sure of ur shm answer?
i will surely recheck....some calculation errors may have crept in !!!!!!!
if the inclination is same for the three cases then- three of them would have the same KE at the bottom
soumik, i donno abt the equivalent constant concept u r talking abt. (havnt done it), can u do it by the longer method or the method wid out eq. spring const.?