no takers?
bhaion aur unki behnon.., plz try it out guyz..
cheers!!
im gonna keep posting some good problems in mechanics from now on. u wudnt find these problems to be really fundu. level or or sumthing, but wud still find it conceptual enuff.some rules u have to follow while doing this will be that u either solve the problems, or post hints, but plz dont give links to any such problem solved earlier. all u jee 2010 aspirants are most welcome to attempt these problems.
1)find the time period of the following set-up
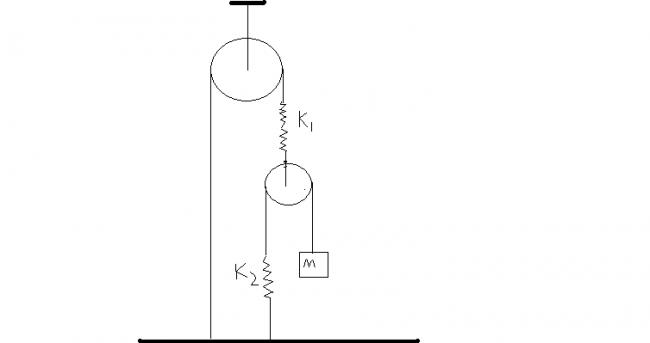
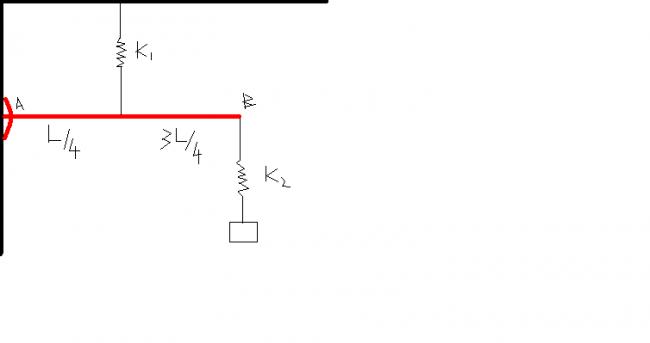
2)find the time period of the following set up.(rod AB is massless)
3) a mass 'm' (particle mass) is left free at the top of 3 different paths A), B) and C), thru' which path wud it have maximum KE when it reaches down, given that the coeff. of kinetic friction in all the 3 paths is 'K'
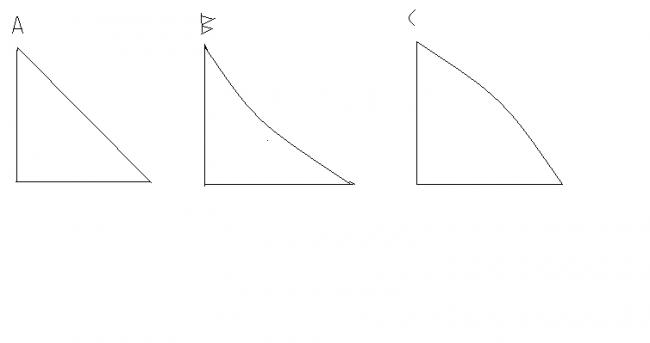
solve these many for now, ill be back with some other prob.s
cheers!!
-
UP 0 DOWN 0 5 40

40 Answers
@smsm, the 3 are of diff. shapes., one is convex one concave, one straight. and + all of them are not friction free..
the height throgh which the three blocks are desending is same i.e. all of them have the same PE intially nd as the mass is same and coff. kinetic friction is also same , the heat produced will be same in all the three cases nd hence the KE should should be same in the three cases(enegy conservation law)
friction is a non conservative force, work done by friction is definitely gonna depend on the path taken. and from the result infact, u will see that. ur answer wud have been correct if and only if there were no friction in the 3 tracks..
hey gordo friction is surely a non conservative force the -work done by friction is always less than dat of the Friction.distance bcos it always accounts with an increase in internal energy of the body as n the reference frame of the block.
u need to view friction in microscopic level u can google it or u can see this in this link http://www.absorblearning.com/media/item.action?quick=50
we have an approximation of work done by friction http://en.wikipedia.org/wiki/Friction the work done by friction will be a complex one if we need to account for the microscopic welds.
okie, ill post the solution to problem 3, while u guyz try 1 nd 2.
hope the situation gets a lot more clearer than it is now after it post it..
luk by any path, say concider the motion of the particle at an angle \alpha to the horizontal,
now as we write the W.E theoram,
work done by all forces= change in KE
so ,
(mgsin\alpha -KN)ds= dE
now concider all cases seperately,
we have for the concave case,
\frac{mv^{2}}{R}+ mgcos\alpha =N
or, we have
E=\int mgsin\alpha ds -K\int mgcos\alpha ds - K\int mv^{2}/Rds
we have mg∫sin(alpha)ds = mgH where H is the height of descent,
similarly we have mg∫cos(alpha)ds= mgL 'L' being the length.
H and L are common for all 3.
now for concave case we have E=mgH-KmgL -K∫mv2/Rds
where R is radius of curvature at any alpha.
coming to the convex case, we have ,
N=mgcos\alpha -mv^{2}/R
and thus, we have
E= mgH - KmgL + K∫mv2/Rds
for the flat case we have at every instant R=∞, so mv2/R=0,
a speacial case of both convex and concave,
so we notice that E the KE at the end pt,
for
1)concave case = mgH- KmgL - ∫Kmv2/Rds
2)convex case= mgH-KmgL + ∫Kmv2/Rds
3)flat case= mgH-KmgL
we know that Kmv2/R at any instant for both convex and concave are different, but are positive,
so we have Kconvex>Kflat>Kconcave
tell if any problem.
cheers!!
guyz plz try the other problems.
asish, soumik, msp, mani,eureka,organic..try it bros.
cheers!!
let the mass be disp. by x .......
let this account for xsp(elongation of spring(k2) and xrod (disp of rod!!!!)
thus
x = xsp + xrod ...
let rod be displaced by a small angle @ ,,,,
therefore xrod = L@ ,,,
elongation of spring k1 is L/4@ !!!!!!
since Irod = 0
0 = K1(L/4 @)L/4 - K2xspL
K1@L/16 = K2xsp
L@ = 16K2xsp/K1 .....
mw^2[16k2/k1 xsp + xsp] = k2xsp
w = √k2/m(16k2/k1 + 1)
//////////////////////////////////////////////////////////////////////////////////////////////////