good question

In time δt and additional length v₀δt starts moving with speed v₀. So the gain in momentum/time = mLv₀² which must be provided by the net force P - (m/L)gy. So
P = mL(v₀²+gy)

Next, the work done by this force as the entire chain is lifted off is
W=\int_0^LP\ \mathrm dy = \int_0^y \dfrac{m}{L}(v_0^2+gy)\ \mathrm dy=mv_0^2+\dfrac{1}{2}mgL
(P.S: The upper limit in the second integration is L and not y)

On the other hand the increase in the mechanical energy of the chain is
\Delta E = \dfrac{1}{2}mv_0^2+\dfrac{1}{2}mgL
So the energy lost is = \dfrac{1}{2}mv_0^2

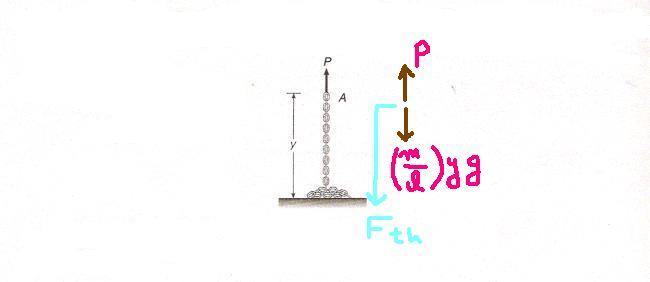
Draw the F.B.D of the hangign part of the chain.
The three forces acting on the hanging chain are; externally applief force P, weight of the hanging portion, and thrust due to the adding of links frm the bottom end.
From variable mass concept, F_th = (dm / dt) x V_rel

Here V _rel = 0 - v = -v and the mass of the main system is increasing.
So, F_th is acting opposite to V.

dm / dt = (m/l) dy/dt =(m/l) gV
Therefore, F_th = (m/l)gV ²

As chain is moving with const velocity, therefore
P = F_th + (m/l) y g
= (m/l) V² + (m/l) y g
= (m/l) [ V² + yg]