6zabardast boss!
A spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance of 5R from the centre of the planet, the spaceship fires an instrument package with a speed V at an angle theta(θ) to the line joining the spaceship and the centre of the planet. The package has a mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
-
UP 0 DOWN 0 0 2
2 Answers
1
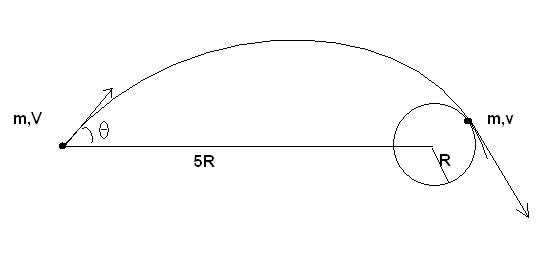
Since the force acting is central, that is, its directed towards the centre of the planet at every instant, the angular moment of the particle about the centre of the planet will be conserved.
that is
mVsinθ*5R=mvR
or v=5Vsinθ ... (i)
Since gravitation field is a conservative field,
the energy will be conserved
or
-GMm/5R +1/2 mV2=-GMm/R + 1/2mv2
or GMm*(4/5R)=1/2mV2(25sin2θ-1) ...using (i)
or \theta =\sin^{-1} \left[\frac{1}{5}\sqrt{\left(\frac{8GM}{5V^{2}R}+1 \right)} \right]