1** for a thin sperical shell field at any point inside it is zero.
so if at B, field is G(say) then at A it shuld be -G.
becoz if u complete the sphere, A and B coinsides..
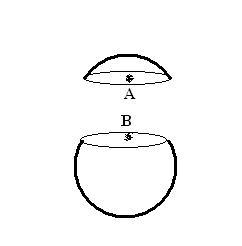
Q. A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in fig. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
-
UP 0 DOWN 0 1 9
9 Answers
62Asish... try this one again ;)
This is more a logical question that a numerical one....
I think this was solved long back on the forum by priyam...
106no idea bhaiyya .. 1 week ho gayaa try karte ... ab nahiin soojh rahaa...
1
66There is one problem with your arguments skygirl. The field gA at A is composed of two parts: field gAA due to part A alone and gAB that due to B at A. Similarly, the field gB is composed of two parts: field gBB due to part B alone and gBA due to part A at B. (All these quantities are vectors). If we complete the shell what we now for sure is that the sum total is zero:
gAA+gAB + gBB+gBA = 0
From here how do you conclude that gAA + gBB = 0? (which is what the question at hand asks.)
106but it says .. gravitational field due to the first part at A and due to the second part at B...
1but when we are completing the full sprhere..
A and B are same..
then gAA and gBA becomes same...
similarly gBB and gAB are same..
so as gAB+ gBA =0 => gAA +gBB =0
66Yes. that's correct; that observation was what I was looking for.
However, by analogy to the hydrostatic pressure, it can be shown quite easily that the gravitational field at the base center of any part of a shell is simply a constant times the cross-sectional area, where the constant is depending (apart from numerical constants) only on universal gravitational constant and the surface mass density. In this case, the base areas are same. Accordingly, the fields must be same.