short cut to problem 1 ,without integration we can do like this
Maybe these are too tough , maybe very easy , but I would definitely appreciate a good solution of these problems ----
Find
1 > The gravitational field on a point mass due to an infinitely unstreachable thread of density p
2 > The grav. field on a pt. mass situated at a height a / 2 from the center of a square plate whose each side is a.
3 > The gravitational compression on a layer of atmosphere situated at a distance r from the center of the earth.
4 > As gravitational and electrostatic vector fields both obey inverse square of distance law ,
then can we apply the same elactrostatic laws to gravitational fields too ? If yes , then how can
we define gravitational flux of a body ? Again , if two or more vector force fields vary with a
certain term equally , then would the laws that are applicable in any one of the force fields , be
applicable to others also ? Moreover , why would this happen , if it happens at all ?
Hey xYz , you have done a blunder .
Gauss's law states that ,
\oint_{}^{}{} g . dS = - 4GmÎ
where g stands for the gravitational flux vector , not the field force .
There is yet another mistake , which is why you are getting 4 in the numerator .You have
messed up in choosing the direction of dS vector.
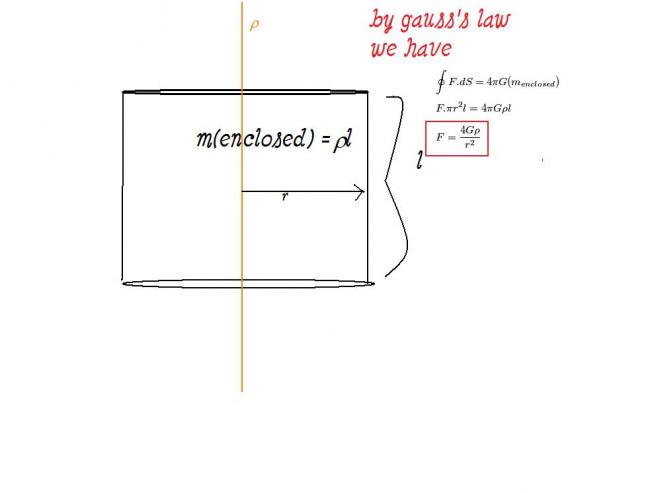
I finally learned Gauss law , so I found out the answers .
Hope everyone tries this one . Else I have to do it myself
xyz is now correct about the 1st question.
g is the gravitational field vector and ∫g.ds is the net flux enclosed.
Gravitaional flux is the number of field lines passing through a given area normally,equal to g.s .
4. yeah,as the gravitational and electrostatic forces are conservative and obey inverse square law,they shall have similar laws.
thats why gravitational and electric field,potential for different bodies(solid sphere,shell etc) are totally similar.
Yup , I was wrong abt the flux thing , but why aren't you trying the 2nd and 3rd one ?
Oh I forgot , yes xYz your answer is correct , but can you explain why you have taken the surface area as 2pi r l , instead of 2 pi r ( l + 2 ) , ( not that it's my doubt ) ?
Arrey yar , very good sol. diya , aur ek kyon nahi ho raha ?
hint. -- how many usable gaussian surfaces can you think of ?
I don't know why you can't do the second one . USE A GAUSSIAN CUBE . oh god !!!
The point mass is at the center , so all the six faces exert equal forces.
ok , can we do it in this way , stretch the point mass into a infinitely long thread of even less mass ,
then we can do it
though the procedure given before could be used , once I get flux of the whole cube I can get the field of the cube too , then divide by six
soumya if divide by 6 ,u will get flux passing thr one face
that u will,,, i told u b4 ....
but please let me know how will you find the field at point stright above the centre of square plate using this flux!!!!!!