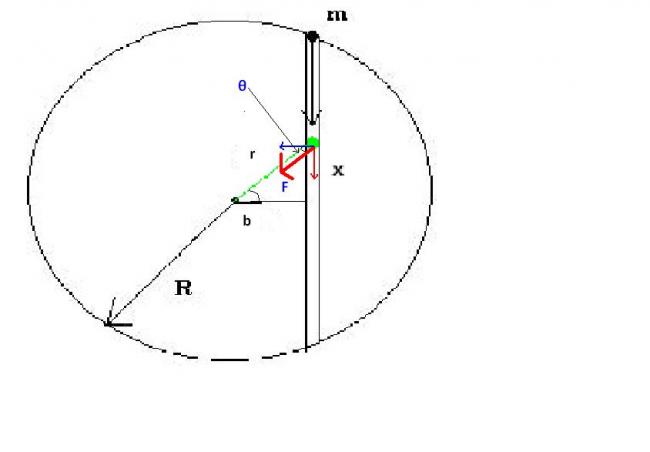
when particle is at a distance r from the centre,
F_{r}= - G \frac{M_{r}m}{r^{2}}
now on drawing FBD , u will find that normal force balances F cos\theta, and only Fsin\theta acts on the body in the direction of 'x'
so F_{net }= F_{r}sin\theta = -G\frac{M_{r}msin\theta }{r^{2}}
where M_{r} = \frac{r^{3}M}{R^{3}}
and sin\theta = \frac{x}{r}
hence\; F_{net}= -G\frac{Mmx}{R^{3}} = -kx
hence the resultant motion is an SHM ( wich is of course)
whose time period will be
T = 2\pi \sqrt{\frac{m}{k}}= 2\pi \sqrt{\frac{m}{GMm/R^{3}}}
T = 2\pi \sqrt{\frac{R^{3}}{GM}}
and \; the\; ans\; to\; the\; ques\; is \;\frac{T}{2}=\pi \sqrt{\frac{R^{3}}{GM}}