3done bfre i guess...
IT WAS ASKED IN IIT 2008 A uniform thin cylindrical disk of mass M and radius R is attached to two identical massless springs of spring constant k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. The unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity V ˆi . The coefficient of friction is μ. Find the net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position..........................................
But in the solution provided by arihant, they showed that angular acceleration was anticlockwise . also in the question nothing is mentioned about initial angular velocity. if we take initial angular velocity equal to zero, then ω at any time will be anticlockwise so it does not satisfy the condition of pure rolling i.e v=ωr. velocity of bottommost point is not zero ........ HOW IT IS POSSIBLE ??????????????????
-
UP 0 DOWN 0 0 2
2 Answers
106
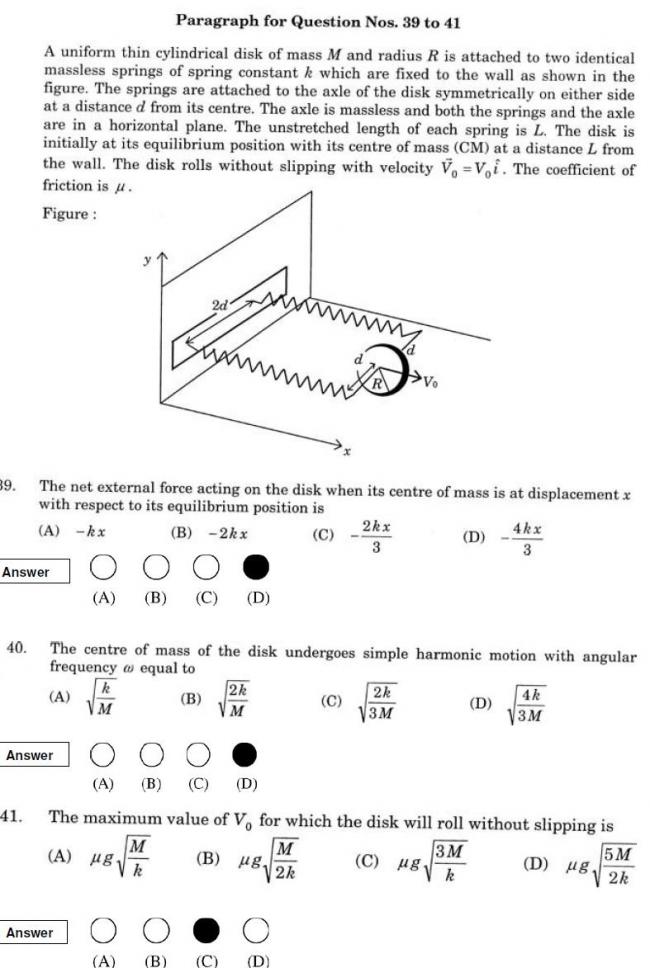
this is the actual question..
initially, the disc is set in rolling motion (given)
so there is initial angular velocity = V0/R
now to maintain that pure rolling, a=Rα must be satisfied.. So,
2kx - f = Ma ... (i)
a = Rα ... (ii)
-fR = Iα = (MR2/2)*a/R ... (iii)
Solving these three we get a= -4kx/3M so F=ma = -4kx/3.
