ok i got the answer when i solved the paper but afterwards i thought....
if initially the momentum is in x axis how can be the net momentum only be in in a perpendicular axis (option b) i am not able to see the impulse......How the ball collide??
The balls, having linear momenta
p1 = pˆi and p2 = −pˆi , undergo a collision in free space. There is no external force acting on the balls. Let
p'1 and p'2 be their final momenta. The following option(s) is (are) NOT ALLOWED for any
non-zero value of p, a1, a2, b1, b2, c1 and c2.
(A) p'1= a1ˆi+ b1ˆj+ c1^k
p'2= a2ˆi + b2ˆj
(B) p'1= c1^ k
p'2= c2^ k
(C) p'1= a1ˆi+ b1ˆj+ c1^ k
p'2= a2ˆi+ b2ˆj - c1 ^k
(D) p'1=a1ˆi+ b1ˆj
p'2 =a2ˆi+ b1ˆj
-
UP 0 DOWN 0 1 17

17 Answers
the collision can be 3D.......
Suno.......
The collision is taking place along x-axis........
But still there are two axes, so after the collision they will surely be in same plane but not on the same axis..they are free they can move anywhere in 3d co-ordinate sys.
Understand.
The answer is A and D.
Coz......If no external force is acting.......the sum of their final momenta and intial momenta must be zero.
P initial + P final=0
now in option B, c1=-c2, then P initial + P final=0
now in option C, a1=-a2, b1=-b2, then P initial + P final=0
For option A, c1 ≠0 as given in ques, then P initial + P final≠0
and for option D, always P initial + P final≠0 as b1≠0.
THE PERFECT ANSWER, ISN'T IT!!
ok leave it!
I GOT IT.....:)
......but still dunno how a collision can be 3D.... but i got this question....
.........but somewhere i cudn understand yet..... i dunno where........ yes this direction part is still unclear.....
how can there be a 3d collision.........??
plz explain.........
yes that is what i am saying precisely..
forget friction for a bit..
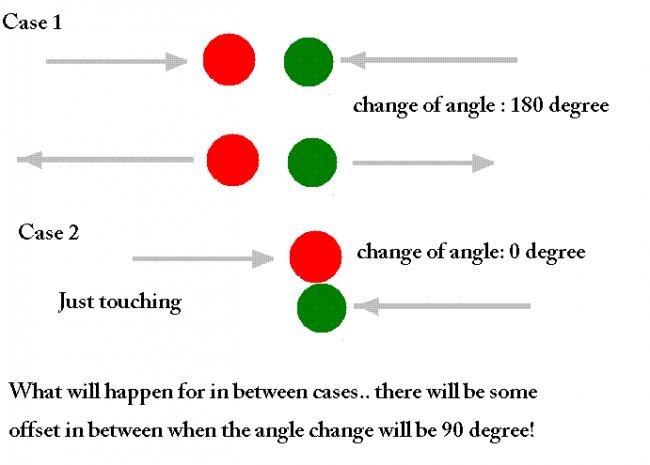
in case 1 red ball returns back...
in case 2 red ball keeps moving front..
in middle cases.. the ball changes angle in between zero to 180°
so there will be a situation when it will change by 90°
So there is no need to think about frictional impulse..
This can be done even without frictional impulse! :)
in case 2:
it can be so that their x components become 0 due to friction
is this possible for a ball to set other in perpendicular directions?
Initaill total momentum is zero..
for conservation of linear momentum u need to check for which cases final momentum can be zero ...
this is obvious for A bcos in z direction momentum is c1 which is non zero! (so no momentum conserved!)
exactly.. if the balls are not running on the same plane.. like if the first ball is slightly displaced to the upper direction..
good explanation nikita :)
Just lift the red sphere a bit above the paper.. so that it still touches the green ball while passing..
okkkkkkkkkkkk!!!!!!!!!!!!!
yes it has to change direction!!!
i thot they were colliding headon ..... but yesss!! dat is never mentioned... thankyou !!
ok , it will be a 2D-plane motion right?
then y not B?
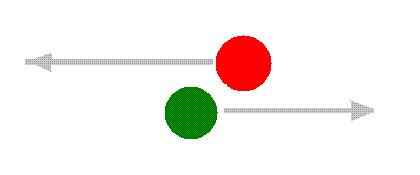
will the two balls continue to move along the same path? or will they change their direction after collision?
dat is my question.........:)
i thot it should be for all..........
well initially there was motion only along x-direction...
so none should be allowed.........acc me.....
explain ......
for D alos, this will be the case..
why.. this is simple!
and why not for B and C?