dude angle is given as 37°
1. plane moves due east at 60 km/h over a city X at a certain time. 12 mins lateranother plane takes off from the station Y which is 40 km due north of the city and flies 37° south of east . if both maintain their direction , find the speed with which second plane must fly in order to strike the first plane
-
UP 0 DOWN 0 0 18

18 Answers
I considered actual values of sin 37 and sin 53.
If u see properly, sin-134 is equal to 36.86° and not 37°.
Hence I was getting the answer as 97.07kmph and not 96.77.
Thnx arshad and philip....u opened my eyes.
ha ha ha....that was funny...i take it u are a big fan of dbz like me.....
i knew but i forgot to use it in this question........forgetting is as good as not knowing...........
dont u know that in a right angled triangle if one angle is 37°
then the sides are 3,4 and 5 respectively
phillip may i ask u why u took vx=4v and vy=3v....
even if we assume vx to be 4v but then how can ve assume vy to be 3v..?
I didnt have the patience to go thru soumyas soln.
but all we need to know is that the horizontal(along east) distance to be covered is 12 km and "vertical"(along south) distance = 40km
also let Vx = 4v and Vy = 3v
we are looking for the value of 5v
equating time to cover distances in both dirs -
124v - 60 = 403v
we get v = 600/31
and 5v = 96.77 km/hr
Yes, Soumya, u're right. I made a calculation mistake.
Is the answer 96.774 ?
soumya your ans is approx. correct . the actual ans is 96.8 but arshad is also correct u should have used the concept of relative velocity
i believe both of u are wrong....u havent taken the concpt of relative velocity in ur solution....
just assume one of the planes at rest by subtracting its velocity from itself and subtracting that same velocity with the direction from the other planes velocity.........
now do that and try again
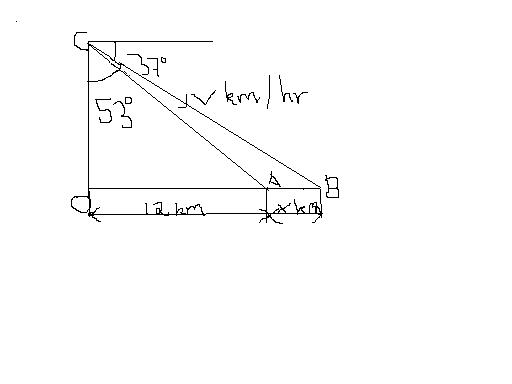
let the first plane starts from o & the 2nd fom c.
in 12 min the first plane travels 12 kms.
let the first plane travel x km before both collide
OC=40km
tan 53°=(12+x)/40 so solving,x=41.08 km
sin 53°=(12+x)/BC so BC=66.46 km
time taken by the first plane to travel ob=53.08/60 =0.88hrs
time to travel AB=time of flight for the 2nd flight=(0.88-0.20) hrs
=0.68 hrs
v=66.46/0.68 km/hr =97.73 km/hr
HOPE IT,S OK!!!!!!!!!
It seems a simple problem of relative velocity...
By the time the second plane is launched, the first one has already covered 12 kms. Now make the first plane stationary and find the required velocity..