262|a_{net}| = \frac{|\vec{\Delta v}|}{t}
|\vec{\Delta v}| = |v\hat{i} + v\hat{j}| = v\sqrt{2} = \sqrt{2}m/s
T=\frac{2\pi r}{v} = \frac{2\pi }{25}s
|a_{net}| = \frac{|\vec{\Delta v}|}{T/4} = \frac{50\sqrt{2}}{\pi } \approx 22.5 m/s^{2}
A particle is moving in a circle of radius 4 cm with constant speed of 1m/s.Find average acceleration in a time interval from t=0 to t=T/4.Here,T is the time period if the particle.Give only the magnitude.(T turns out be about 25.12 s).
-
UP 0 DOWN 0 0 5
5 Answers
262
158the correct answr given is 0.23cm/s2.....i hv tried to solve it this way...
T=ds
d=circumference of circle
=25.12cm
s=1cm/s (given)
thus,T=25.12s
and,T4=25.12/4
=6.28s
average velocity from t=o to t=T/4=displacement /time
=AB/6.28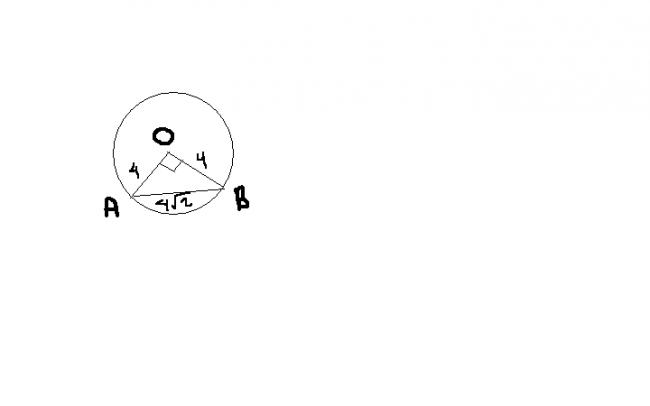 
(A and B are the points of a circle with centre O and radius 4 cm and angle AOB=90 degrees)
=4√2 /6.28
=0.898cm/s
now,at t=0,v must be 0
thus,average acceleration=change in velocity/time
=(0.89-0)/6.28
=0.89/6.28
=0.142cm/s2.......which is far away from the given correct answer
49Whatever Aditya did was perfect. He just screwed up his unit calculations and units used.