i have a doubt in the first question........ if the acceleration is very high won't the 2 blocks get separated!!!
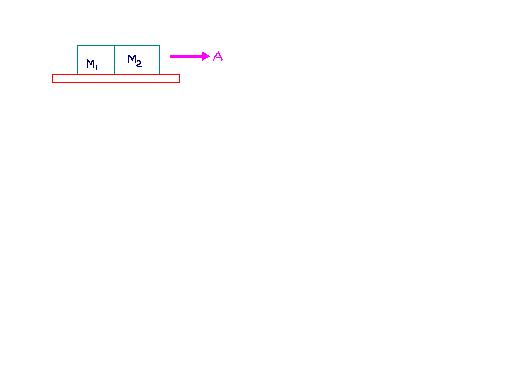
Ques1) Two blocks of masses M1 and M2 (In the above figure) are placed in contact with each other as shown. The voefficient of friction b/w M1 and platform is 2\mu and that b/w block M2 and platform is \mu . The platform moves with the acc a. Show that the normal reacn b/w the blocks is non zero if a>\mu g.
Ques2) 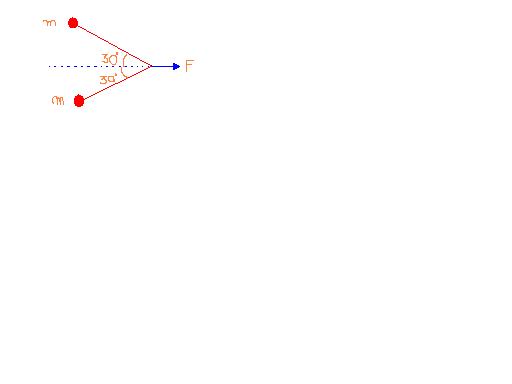
IOn the fogure two identical particles each of mass m are tied together with an extensible string. This is pulled at it's centre with a const force F. If the whole system lies on a smooth horizontal plane, then show that the acc of each particle towards each other is F/(2√3m).
Ques3) 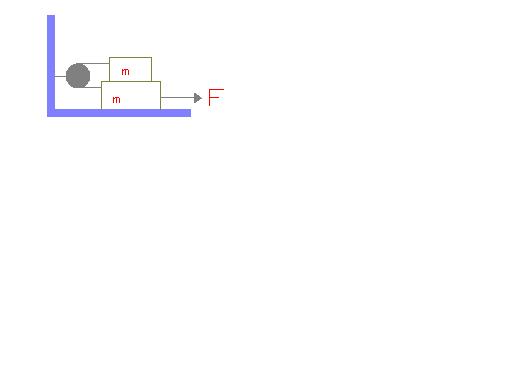
For the arrangement shown in the figure the coefficient of friction b/w the two blocks is \mu . If both the blocks r identical, then show that the acc of each block is (F/2m) - \mug.
-
UP 0 DOWN 0 0 5

5 Answers
the 2nd question.....it can be solved by taking components of the force.....
Q1) Take the reference frame that is fixed to the platform. In this reference frame there acts a pseudo force to the left on both the blocks: m1a on the left block and m2a on the right block.
If a < μg then obviously a < 2μg.
But then m2a < μm2g = f2,max. Therefore, in this case the friction force f2 between the mass m2 and platform, which is a self adjusting force, acting on block 2 towards the right is enough to balance the (pseudo)force m2a. And so it wont press against the block 1. As such the contact force between them will be zero. In this situation obviously the friction force on block 1 is also balancing m1a.
As such, for the contact force between them to be non-zero which will happen when f2 achieves its maximum value, we must have a ≥ μg.
However, lets see how does the blocks move if we do indeed increase a from its minimum value of amin=μg.
Then, m2 is pressing against m1 though the system still does not move. The friction force between m2 and the platform is μm2g (since it has achieved its maximum value.) However, f1 (friction between m1 and platform) can still increase. Due to equilibrium of m1 and m2, we get
the contact force between them as
N = m2(a-μg).
And
f1=m1a+N = (m1+m2)a - μm2g
This force achieves its maximum when f1 = 2μm1g, i.e. when
a = m2+2m1m1+m2 μg
At this instant the mass m1 gives way as well. How do u think the blocks will move after this?
Q2) The acceleration of each mass towards each other will be caused by the component of the tension in the thread. If the tension be T, then we have
2Tcosθ = F
giving T = F2cosθ
I have taken the angles shown as 30° as θ.
The component of this tension providing the acceleration towards each other is T sinθ. Therefore, the required acceleration
a = T sinθm = F tanθ2m = F2√3 m
Q3) Draw the FBD's of each block. Because of the thread, they will have the same acceleration (in magnitude) in opposite direction. The force of friction will act in the forward direction on the upper block and in the backward direction on the lower block. We then have
for the lower block: F - T - f = ma
for the upper block: T - f = ma
Adding, we get
F-2f = 2ma
Since there is sliding friction, f = μmg
Hence we have
F - 2μmg = 2ma
from where we get
a=F2m - μg