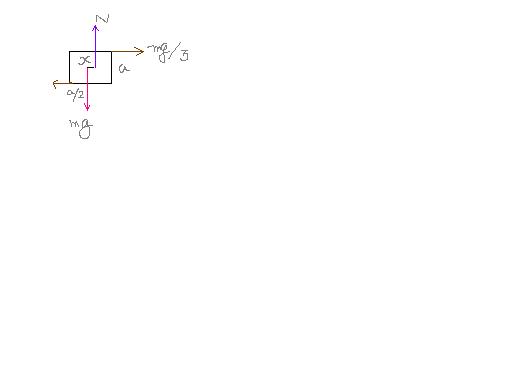
See, the point of application of the normal reaction is displaced through x bec to produce a clockwise torque abt the centre of mass that may balance the anticlockwise torque produced by the frictional force.
In other words, the normal reaction is acted at a distance x bec a horizontal force F is applied. So for =lbm, N is acted at a distance x in anticlockwise direction.
For toppling (rolling ) of the body, slipping of normal reaction is required at a point or the line of contact to the max value.