Laws of Motion

The acc. of the two bodies are along different lines, so they cannot be directly subtracted........

From the figure,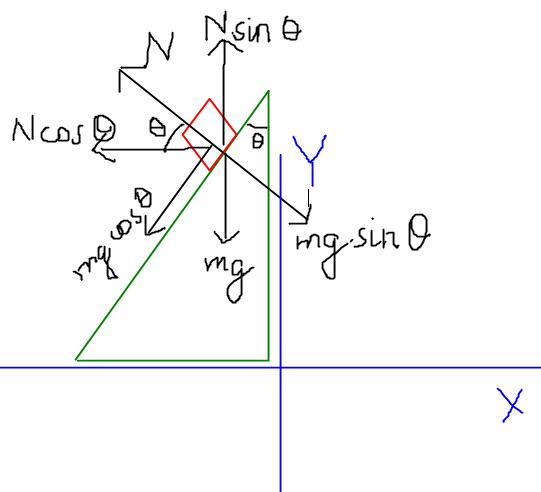

mgsin@=N

F_x=Ncos@=mgsin@cos@

F_y=mg-Nsin@=mg(1-sin²@)=mgcos²@

In the given problem......

a_1x=(g/2)sin2@=(g/2)sin60°
a_1y=gcos²@=gcos²30°

a_2x=(g/2)sin2@=(g/2)sin120°
a_2y=gcos²@=gcos²60°

Therefore acc of second wtr first,

a=(a_2x-a_1x)i+(a_2y-a_1y)j
=(g/2)(sin120°-sin60°)i+g(cos²60°-cos²30°)j
=0i+g(-1/2)j
=-(g/2)j

Hence, relative acceleration of the second particle wrt first=\a\=g/2

[339]

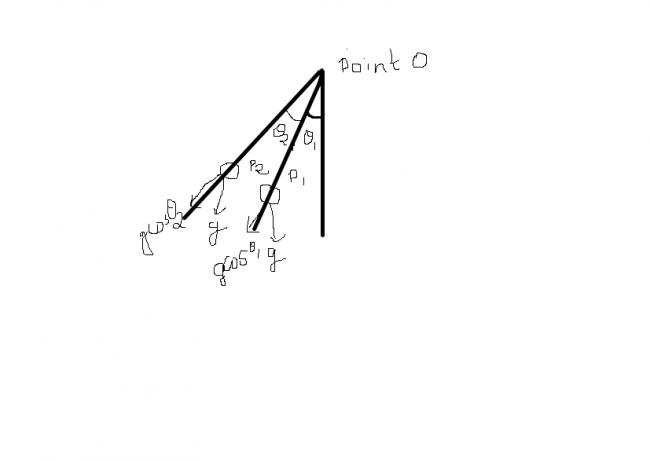
now component of gcos@1 along the second wire is
(gcos@1)cos@2

so component ob 1st particles accn along the direction of second particles accn will be (gcos@1)cos@2

now particles 2's accn along the 2nd wire=gcos(@1+@2)

so relative accn of particle 2 with respect to particle 1 will
be=gcos(@1+@2)-(gcos@1)cos@2

now putting values
from the above question
@1=30°
@2=30°
=gcos60°-(gcos30°)cos 30°
=(1/2-3/2)g
=-g/2
ie the 2nd particles accn will be in the backward direction with respect to the 1st particle with magnitude g/2
=

and kalyan i dont know what hav u done.....what diagram hav u drawn.......???

@arshad

Well, I just drew the FBD for one general particle

and found the forces along X and Y axis in this general case.

Substituting this in the two cases, I got the Forces along the axis for the two particles and subtracted, that clearly gives the relative acceleration...

I started off with your method by taking a component and solving, which gave me an answer...

But I got into a confusion at one point!!!

When @₁+@₂ = ∩/2,
A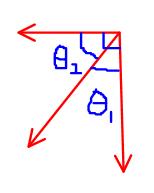

g

There is still a component of g in the direction of A = gcos@₁@₂

While in real sense this component is supposed to be zero (gcos∩/2)

In a way, you can continuously use n number of @s to get a component of g in any direction, while this is not possible practically

So that made me think, U cant take components of a component, and forced me to look for another way to solve this problem, and the above method struck me!!!

[5][5][5]

my explanation

since the particles are sliding on wires their compnent of g perpendicular to the wires will be balanced by the normal .

thus only g sinθ is thw resultant of the particles .

therefore

a₁ = - g4 i - g√34 j

a₂ = -g√34i - g34 j

a₂₁ = a₂ - a₁
= -g(√3-1)4 i - g(3-√3)4 j

is it correct?