13options[12]
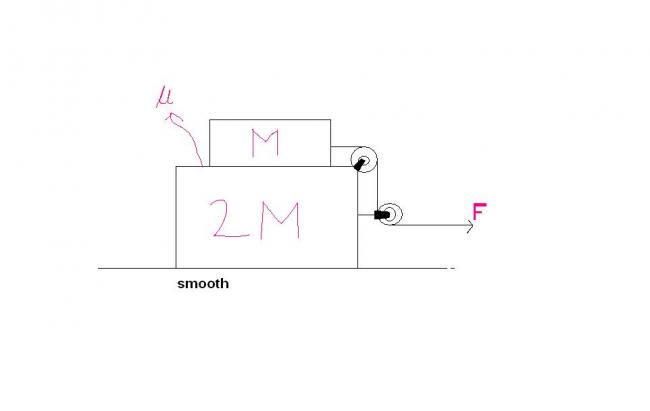
find the minimum value of μ between the two blocks for no slipping
-
UP 0 DOWN 0 0 9
9 Answers
106As there is no slipping, consider the block of mass m,
F-μmg = ma ....(i)
μmg=2ma ....(ii)
So, a=μg/2
Putting in (i),
F=3μmg/2
==> μmin = 2F/3mg
..........i am not sure abt my process but do verify.
24aA+B=F/3m
=>aA=F/3m
Force eqn for upper block (A)
F-f=maA
=>F-f=F/3
=>f=2F/3 ≤ fmax
=>F≤3μmg/2
1
don't u think that ther will be a force acting on bigger block through string
106yes, it definitely will but see the attached FBD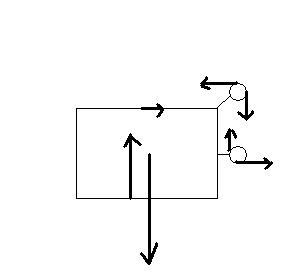
there will be in all 4 forces by the string.... as u can see from FBD, all 4 cancel each other.