A uniform rod is made to lean between rough vertical wall and the ground.Find the least angle at which rod can lean without slipping.coefficient of friction between rod and wall is 1/2 and rod and ground is 1/4
-
UP 0 DOWN 0 0 1
1 Answers
11
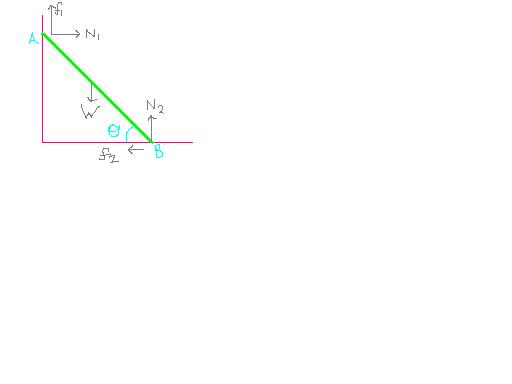
Ans) Let the least angle be \theta. As the road is leaned, it t ends to slip down the wall and towards the right on the ground. As the body is at rest, the net force on the rod is zero. Therefore, f1 + N2 = W. and, f 2 = N1. \mu 2 N2 = N1 N 2 / N 1 = 1 / \mu2 As the body is also in rotational equilibrium, net torque about any point is zero. Therefore, (W/2) Cos \theta = N1 Sin\theta + f1 cos\theta Tan \theta = (w-2f1) / 2N1 Also, w= f1 + N2 and N 2/N 1= 1/ \mu2 On substituting, Tan\theta=(1/2) [(1/\mu 2) - \mu1] {where \mu1 is the coefficient of friction b/w rod and wall and \mu2 is the coeff of friction b/w rod and the ground.} On putting values we get Tan \theta=7/4 Therefore the least angle should be \theta = tan-1 (7/4)