Solid Cylinder, rolls over horizontal surface Find the max value of v which still permits it to roll over incline plane without a jump, sliding is absent.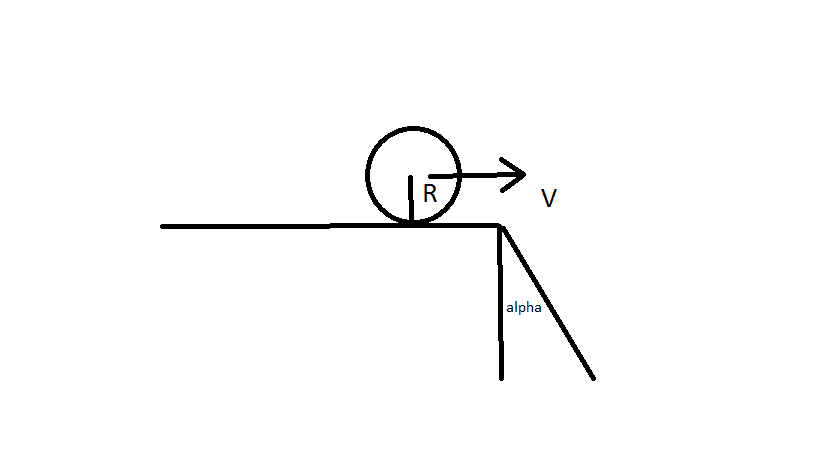
-
UP 0 DOWN 0 0 1

1 Answers
Let v_i be the initial velocity and v_f be the final velocity.
When it is at the edge (where the plane bends down) the ball rotates about that point and then continues to move down the incline.
While rotating,
\frac{mv_f^2}{r}=mg\sin\alpha -N
From energy conservation we get,
\frac{1}{2}I\frac{v_f^2}{r^2}-\frac{1}{2}I\frac{v_i^2}{r^2}=mgr(1-\sin \alpha)
From parallel axis theorem we get I = 12mr2+mr2=32mr2
When the ball is just about to jump N=0.
N=0\rightarrow \frac{v_f^2}{r}=g\sin\alpha
\frac{3m}{4}(v_f^2-v_i^2)=mgr(1-\sin \alpha)
\rightarrow v_i^2=gr\sin\alpha -\frac{4}{3}gr(1-\sin\alpha)
\rightarrow v_i=v_{max}=\sqrt{\frac{gr}{3}(7\sin\alpha - 4)}