mechanics

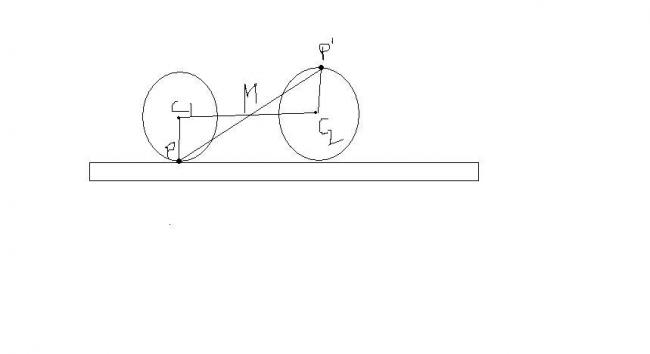
horizontal dist travelled by the center of the wheel = (pi)R

now C₁PM and C₂P'M are congruent....

so C₁M = C₂M = (pi)R/2

so PP' = 2 √(R(pi)/2)² + 1

so PP' = 2R √(pi)²/4 + 1

PP' = 2 x 45 x √3.4649 = 90 x 1.86 = 167.53cm...ans

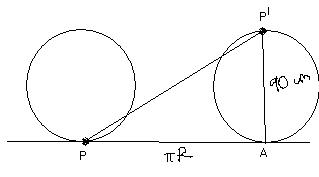
since the wheel has made half revolution so distance covered ( PA ) = \pi R = 3.14 x 45 = 141.3 cm

but we need PP'
so we apply pythagoras theorem for ΔPP'A
we have PP' = \sqrt{(90)^{2}+(141.3)^{2}} = 167.52cm

now angle relative to horizontal is angle P'PA
so we use sinθ = 90167.52 = 0.537
θ = sin^-1(0.537) = 32.4°

hence required are
(i) magnitude - 167.52 cm
(ii) angle = 32.4°

that line in the diagram is tangent which has wrongly been drawn by me bcoz i'm no perfectionist in drawing

A girl throws a ball at a vertical wall 4m away. The ball is 2m above the ground when it leaves girl's hand with an initial velocity of v₀=14.14m/s and an angle 45° above the horizontal(vx=10m/s and vy=10m/s). When the ball hits the wall, the horizontal component of its velocity is reversed, while the verticle component remains unchanged. How far from the wall does the ball hit the ground????? (a)19.3m (b)18.2m (c)17.0m (d)15.9m

TWO LARGE CRATES M₁ AND M₂ ARE CONNECTED TO EACH OYHER BY A STIFF MASELESS SPRING. THE FORCE CONSTANT OF THE SPRING "K" IS 8000N/m ,M₁ IS 650 Kg, M₂ IS 490 Kg . A CONSTANT HORIZONTAL FORCE "F" IS APPILED TO M₁ WHICH ULTIMATELY GIVES THE TWO MASSES ANT THE SPRING A COMMON ACCELERATION ON THE FRICTIONLESS FLOOR. . IF THE SPRING IS COMPRESSED 5cm FROM ITS INITIAL UNSTRETCHED LENGH DURING THE MOTION, WHAT IS THE MAGNITUDE OF THE APPLIED ORCE???