Mechanics Booster-7

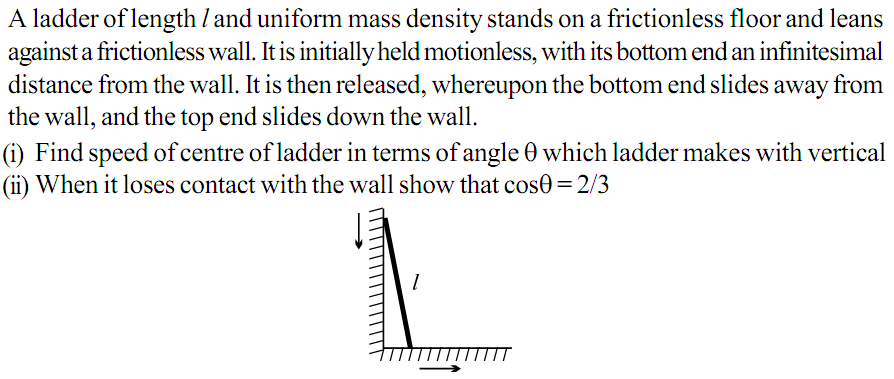
Let the reference point be intersection of the wall and the floor, call it 'O'.
Note: the locus of the COM of the rod is a circle of radius l/2.

Conserving energy about O,
mgl2(1 - cosθ) = 12mv² + 12I_comw²
w = 2vl
Solving,
v = √[3gl(1 - cosθ)4]

Now v_x = vcosθ
As θ increases, v_x acquires a local maximum, and then it decreases.
In short,
dv_xdθ > 0, θ < cos^-1(2/3)
dv_xdθ < 0, θ > cos^-1(2/3)

Normal reaction was from the wall was acting to the right till θ = cos^-1(2/3) increasing the velocity. When θ > cos^-1(2/3), v_x starts decreasing => normal reaction is acting to the left which is impossible. Hence it loses contact at that angle.