A particle moves along the x axis, so that its potential energy U depends on its position coordinate x as
U(x)=A|x|^n
where A is a positive real and n>0. How will the time period of oscillations depend on the total mechanical energy E of the particle?
1let E be the total energy and x0 be the amplitude.
so,
\frac{1}{2}mv^{2}+Ax^{n}=E.
so, we have that
v=\frac{dx}{dt}=-\sqrt{\frac{2E}{m}\left(1-\frac{A}{E}x^{n}\right)}
this implies :
\int_{x_{0}}^{\sqrt{\frac{m}{2E}}}{\frac{dx}{\sqrt{1-\frac{A}{E}x^{n}}}}=-\frac{T}{4}
putting
T=-2\sqrt{2}mE^{-\frac{1}{2}}\left(\frac{E}{A}\right)^{\frac{1}{n}}\int_{1}^{0}{\frac{dz}{\sqrt{1-z^{n}}}}
so, T \alpha E^{\frac{1}{n}-\frac{1}{2}}
3sir ive got 1 doubt ................at max. amp. v = 0 .... therefore we can put x0 in rajats answer as (E/A)^n ..... and at mean position U is min .. or =0 therefore we just have to integrate frm
(E/A)^n to zero na ............ y has he put root(m/2E) and all that stuff ... didnt get it ...
66Yes, iitimcomin, you are correct. Rajat might have done some mistakes. However his final step remains true.
Basically, the potential energy curve is going to be symmetric about the vertical axis. Something like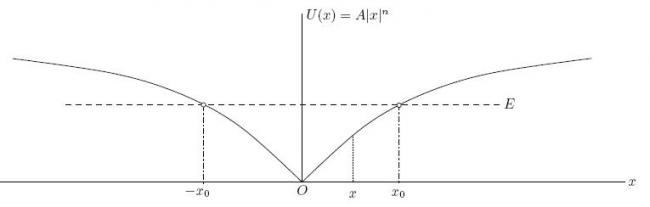
It is easily seen that the time period will be four time the time required to go from x0 to O. That's what you were saying iitimcomin, isn't it?
1Sir, is Rajat's final answer correct?
I got something else.
{I might have made a mistake--------- you know how good I'm at making mistakes :-) }
66yes his final conclusion is correct (the numerical constant might be off a factor of 2) let me check.