or does it show that the rotation is anti-clock wise...!!
q) Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particles system is the same whatever be the point about which the angular momentum is taken.
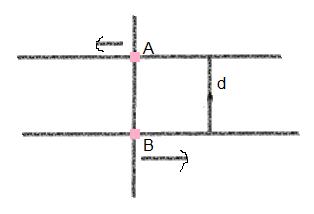
Now my problem is if we look from A then
l = mv(i) x 0 + mv(-i) x d(j) = - mvd
and again from B then,
l = mv(i) x 0 + mv(-i) x d(j) = - mvd
my doubts
1. it means that the direction of j must always be outwards from our point of sight.
2. in above results its -mvd which shows that the direction of angular momentum is downwards
but if i apply right-hand thumb rule then it seems to be upwards
where am i confused can someone please help?
-
UP 0 DOWN 0 0 5

5 Answers
well one more thing can someone prove it when A and B are not mirror images of each other and the point of sight is a point outside the two parallel lines which too is not a mirror image of either of the points?
dont u think when ur looking from A
ur equation should have d(-j) ??
in the first equation??...
just guessing
Firstly,
Angular momentum is \vec{L}=\bf{\vec{r}} \times m\vec{v} . So the products that you have carried out have their signs reversed.
Secondly,
The direction of \vec{L} will be out of plane and always constant because the perpendicular distances as well as velocities remain constant.