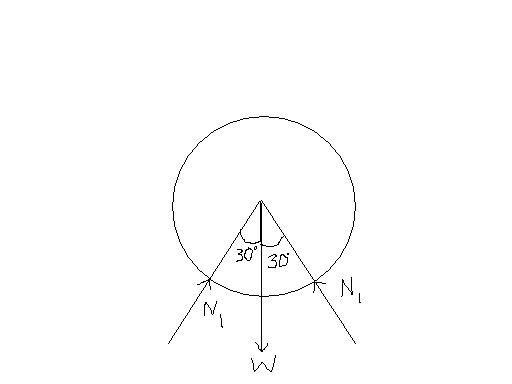
Is it ∩/4?
all surfaces are frictionless. three cylinders are placed as shown in the diagram. find the least angle θ that prevents the arrangement from collapsing
1. tan-11/2
2.tan-11/2√3
3.tan-11/3√3
4.tan-11/4√3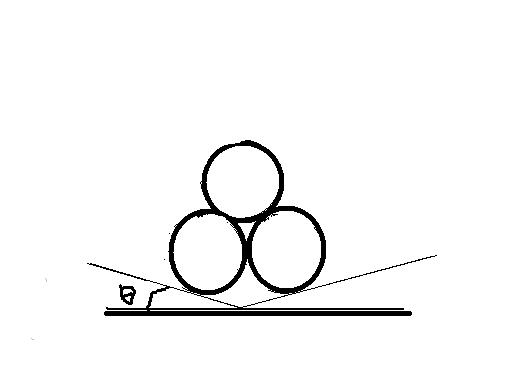
this is for 2010 aspirants..seniors plz dont post solution now.
-
UP 0 DOWN 0 0 16

16 Answers
sorry virang, i've given the options. anyway, post ur method, maybe ur method is right and have made mistake in calculations.
Mg is the downward force of the top cylinder pushing it downwards
This force pushes the two cylinder upwards
Therefore
Mg = √(2p2+2p2cos180-2θ)
The force which keeps the cylinder stable is mgsinθ
p - mgsinθ = 0
mg/√(2-2cos2θ) - mgsinθ = 0
1/√2*2sin2θ = sinθ
1/2 = sin2θ
Sin θ = 1/√2
θ = 45°
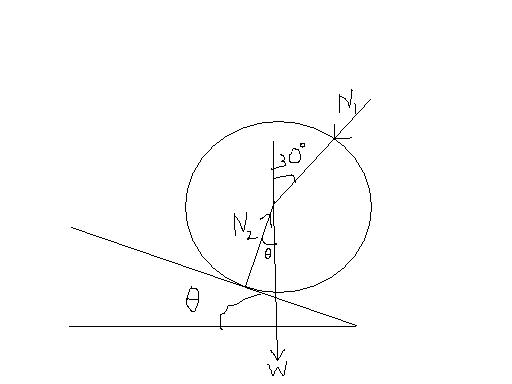
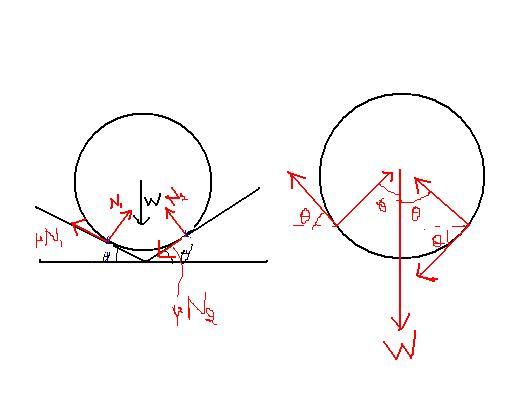
N2sinθ=N1sin 30..............(2)
N2cosθ=N1cosθ + W.........(3)
when they are just not collapsing the two cylinders at the bottom dont exert any forces on each other.
dividing (2) and (3) we get tanθ=1/3√3
or θ=tan-11/3√3
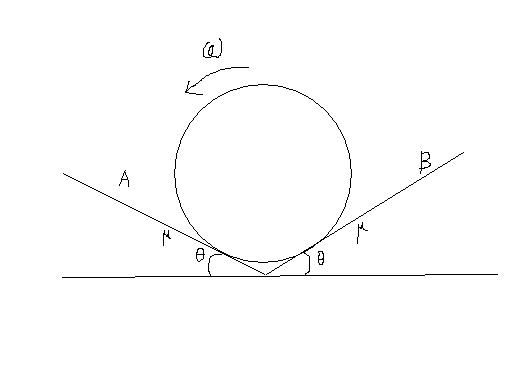
if the coefficient of friction is μ, find the normal reaction N1 and N2 offered by surfaces A and B on the cylinder.
the cylinder is not in equilibrium
ω is the initial value... u have to find out the normal reaction at the initial instant of time..
N1cosθ+N2cosθ+μN1sinθ-μN2sinθ = W ... (i)
N1sinθ = N2sinθ+μN1cosθ+μN2cosθ ... (ii)
sorry for wasting ur preious time, forgot to mention that the cylinder is not in equilibrium....
i mean to say, it tends to roll....
i'm not sure whether the situation is possible, but the ans i got is
N1= mg(1+μ)
.....................
2sinθ(1+μ2)
N2= mgμ
...................
2sinθ(1+μ2)
pls forgive me if my ques is wrong.