1i cudnt get the picture
are the discs standing or are they kept flat on the surface?
and , should we consier the rotational motion also?
you have written small discs
two small identical discs, each of mass mlie on a smooth horizontal plane. The discs are interconnected by a light non deformed spring of length l and stiffness x. At a certain moment one of the discs is setin motionin a horizontal direction perpendicular to the spring with velocity v.F ind the maximum elongation of the spring in the process of motion, if it is known to be considerably less than unity.
how to solve the problem using reduced mass concept
-
UP 0 DOWN 0 0 9
9 Answers
11draw the picture in paint and save it
and then click on the "upload image" button after clicking on add post
3
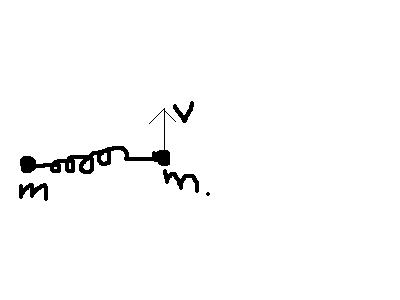
the spring is perpendicular to the velocity vector and the spring is placed on a flat smooth surface sir. i am waiting for your reply sir
1ok
the reduced mass of the system=1/(1/m+1/m)=m/2
we can consider one end at rest and the other end with mass m/2 at a distance L initially
as ther is no torque abt the fixed point
angular momentum can be conserved
at any moment let the distance of the m/2 mass from the point =L+x
then radial velocity of mass = d(L+x)/dt=dx/dt
also when x is maximum ,dx/dt=0
hence radial velocity =0
let tangential velocity be u
then conserving i) angular momentum
(m/2)vL=(m/2)u(L+x)
and conserving energy
(m/2)v2/2=(m/2)u2/2+kx2/2
solving the two above equations we can get x
