Rotation

BITSAT Help › Mechanics questions › Rotation

A uniform cylinder of radius R is spinning about its axis to an angular velocity w₀ and then placed in a corner.The coefficient of friction beween the orner walls and the cylinder is k.How many turns will the cylinder accomplish before it stops.

#Physics #Mechanics

UP 0 DOWN 0 0 4
Post on FacebookPost anonymously?

4 Answers

qwerty ·2011-02-04 00:27:04

Rw(1+k²)4Ï€g k(1+k)?????????????????????

UP 0 DOWN 0
Post on FacebookPost anonymously?

Vinay Arya ·2011-02-04 03:35:06

Dear Account Blocked
It should be w raise to the power 2.And 8 in the denominator.Rest is absolutely correct.And would you like to show me your working?

UP 0 DOWN 0
Post on FacebookPost anonymously?

qwerty ·2011-02-04 04:15:12

oh yeah ! sorry for that error !! ( i wrote energy as Iw lol )

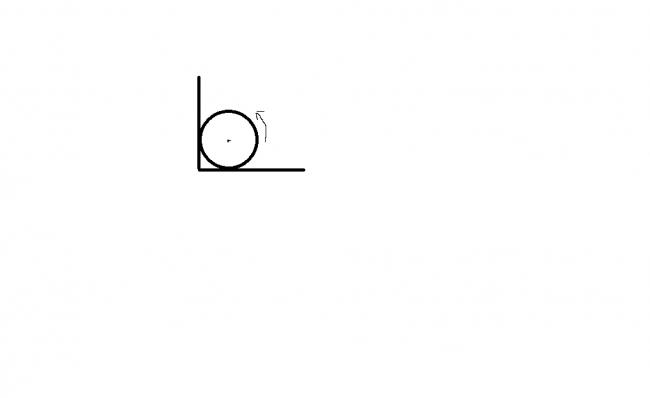
let normal and friction due to horizontal surface be denoted by 1 and due to vertical surface be denoted by 2

mg = N1+f2

N2=f1

f1=Î¼N1, f2=Î¼N2=Î¼f1

so Î¼mg = f1(1+Î¼²)

and (f1+f2)RÎ¸ = 1/2 I w²

then no of rotations = theta /2pi

u will get ans = Rw²(1+Î¼²8pigÎ¼(1+Î¼)

UP 0 DOWN 0
Post on FacebookPost anonymously?

Vinay Arya ·2011-02-04 04:43:37

Thank you very much.

UP 0 DOWN 0
Post on FacebookPost anonymously?

Your Answer

Basic Integral Calculus Operators Symbols Matrix Cases

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω

Close [X]

Rotation

4 Answers

Your Answer

Add Image

Similar Questions