Rotation

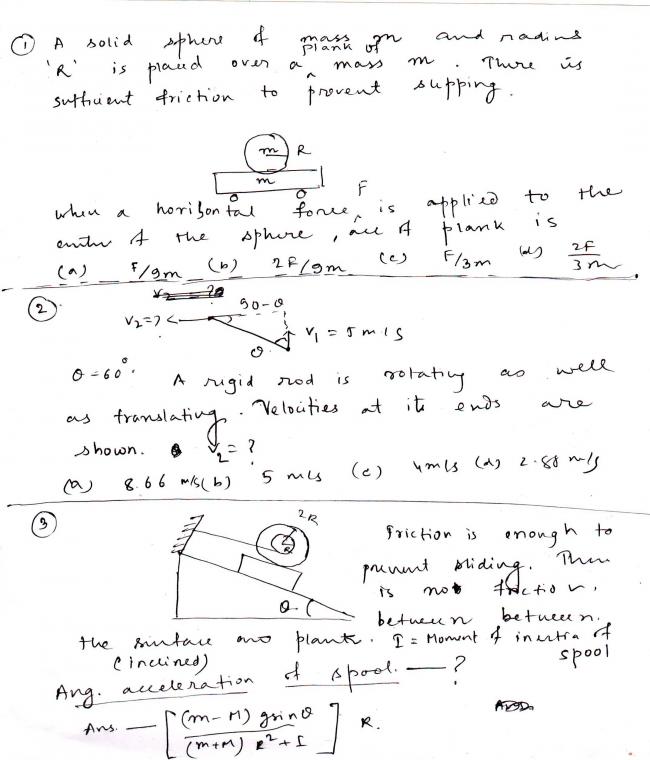
for first question ,

find accn of com of sphere a_s ( 1)

then write torque of friction f abt com and find α (2)

then write accn of plank a_p (3)

as there is no slipping , accn of bottom most point of sphere doesnt move wrt plank
hence accn of bottom most pt = accn of plank (4)

4 eqns , α,a_s, a_p, f , 4 unkowns , so u can get a_p

for 2nd one

v_p = v_p/c+ v_c

i.e accn of any pt p = accn of p wrt com , + accn of com

motion of rod can be broken as pure rotation abt com + pre translaton of com

hence v_p/c = ω x r = rw , wich is _|_ to r

now for bottom most pt of rod ,
write its velocity in 2 components , one _|_ to rod , and another along the rod ,
so one _|_ to rod will become rw , one along rod will become v_com

and then for topmost pt u can use v_p = v_p/c+ v_c

where v_p/c wil be again rw

i think 3rd ques is similar to 1st , use that vel of bottommost pt shud be zero relative to plank, i think that shud do it