A uniform solid sphere of mass m and radius R is kept on a long plank which is moving with acc. a= kt2 , where k = 1 m/s4 and t is time in seconds . There is no slipping b/w sphere and plank . The minimum value of coeff. of fricn. µ b/w plank and sphere so that sphere will slip at t=2s.
i hav formed the reqd. eqns but still stuck!!
i proceeded like this:
ac(acc. of center of sphere ) + Rα = a
f = 2/5 MRα
f ≤ µMg
but how to find ac??
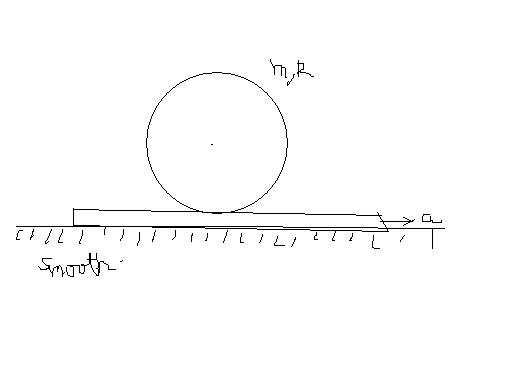
23friction will act towards right
now f = mac
f = 2mRα5
5ac2 = Rα
accn of lowest pt = Rα + ac = 7ac2
fmax = μmg
hence (ac)max = μg
as the sphere shud sleep at t=4 , (ac)max shud occur at t = 4 , after that slipping starts
hence 7ac2 ≤ 4k , i.e 7μg2 ≤4k
μmin = 8k7g
