rotation and changing mass

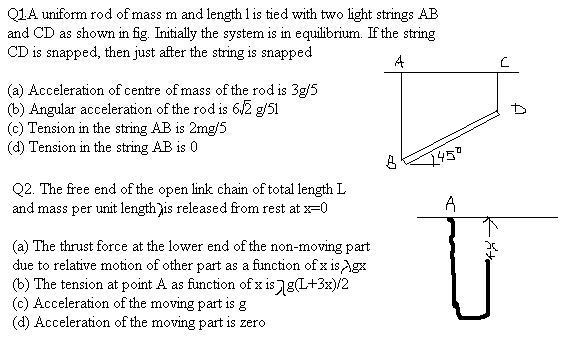
Q1) Just after the thread CD is cut, let the tension in the thread AB be T. Taking the torque about the center of the rod, we get T\sin45^\circ \dfrac{\ell}{2}= \dfrac{1}{12}m\ell^2\beta
where β is the angular acceleration of the rod. This gives
T=\dfrac{m\ell\beta}{3\sqrt{2}} ------ (1)
Along the vertical direction, we get
mg-T=ma_c -------- (2)
Now, the acceleration of the point of the rod which is tied to the thread must have zero acceleration along the thread, so we get
a_c=\beta\dfrac{\ell}{2}\cos45^\circ=\dfrac{\beta\ell}{2\sqrt{2}} ------- (3)
So we get from (2)
mg-\dfrac{m\ell\beta}{3\sqrt{2}}=ma_c
And using (3), the last equation gives
a_c=\dfrac{3}{5}g
And from (3), we get
\beta =\dfrac{6\sqrt{2}}{5}\dfrac{g}{\ell}
And finally we get the tension as
T=\dfrac{2}{5}mg

Well, it will be at rest initially. But it would still have an acceleration. In fact, it is going to move in a circle. So it would have a centripetal acceleration towards A and a tangential acceleration. However, initially its velocity is zero, that's why I put the centripetal acceleration (i.e. the acceleration along the thread) to zero (equation (3)) in my last post. But it would still have a tangential acceleration which you could use to determine, for example, the initial angular acceleration of the thread AB.