11
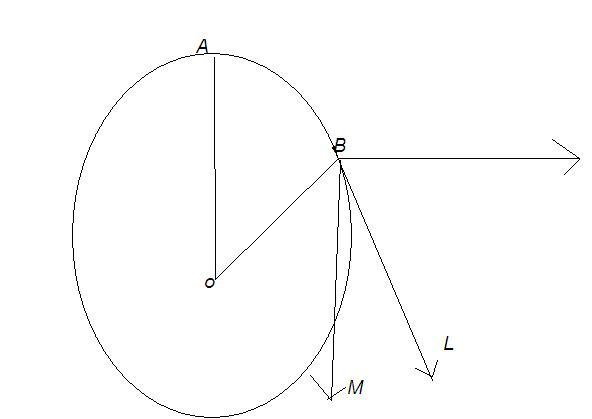
θ=ωt=vr.t
So tangential velocity along BL is v...and centre of mass vel is v as well, angle between these 2 vectors is θ, so evaluate the resultant velocity....
A hoop of radius r rolls over a horizontal plane with constant velocity v without slipping. The velocity of any point on the hoop t seconds after it passes the top position is
-
UP 0 DOWN 0 0 4
4 Answers
11
19the path of a point on the circumference is a cycloid and the distance moved by this point in one full rotation is 8R (R= radius of the circle)
from the figure: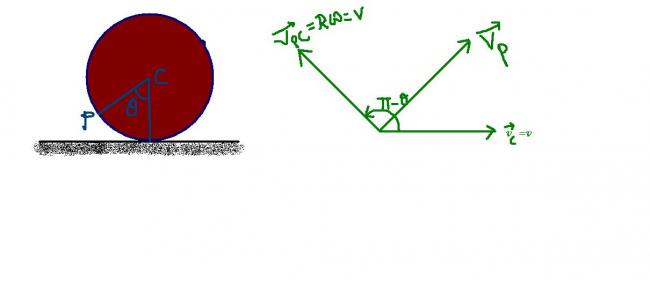
VP = VC + VPC
=> | VP| = √(V2 + V2 +2.V.V.COS(∩-θ)
= 2V sin θ/2
please take care because i have considered the bottommost point as the start !!
33u hav to find in terms of t (time after it passes from top.)
19i missed the point....but it is simple from the point i left !!!!