1no..answer given is √31/8 v
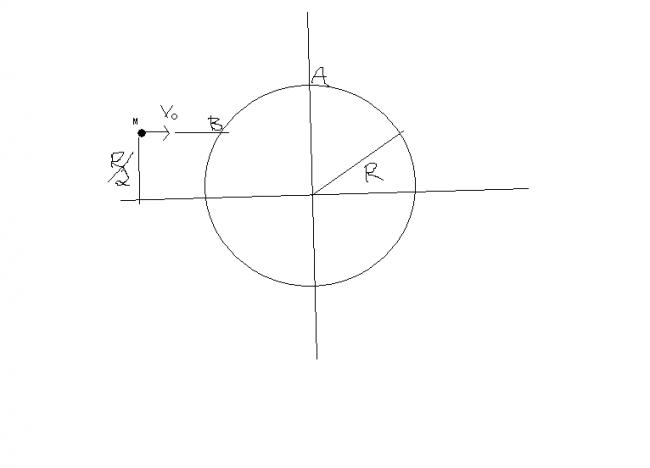
A disc of mass M and radius R is lying on a smooth horizontal surface.A particle of mass M moving horizontally with a velocity V collides with the disc at B and sticks to it.Speed of point A on the disc just after impact will be??
-
UP 0 DOWN 0 0 4
4 Answers
1ok
First of all.
V_c = V/2
then conserving angular momentum about the centre of the disc.
MVR/2 = 2MV_cR/4+I_c\omega
plug Ic and Vc in eq 1 and tell if you can carry on from there ?
1HINT:the point diametrically opposite to A is instantaneous point of rotation. apply conservation of mechanical energy
i havent tried the prob but i think this should do
1n translation motion the direction of linear momentum and velocity are same in all cases
but in rotational motion about fix axis the direction of angular momentum and angular velocity are same if body is symetric and their direction are diffrent if body is not symetric.
the above statement is true or false.
[source NCERT]