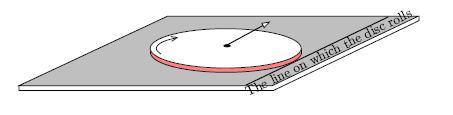
Q1. A uniform disc of radius r is spinned about its axis to an angular velocity ω and then carefully placed with its plane on a rough horizontal surface. Find the time taken for the disc to stop rotating, given the coefficient of friction between the disc and the horizontal surface is μ. Assume that the disc exerts pressure on the horizontal surfcace uniformly.
-
UP 0 DOWN 0 0 36

36 Answers
◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘
Q2.
J =3mv/2
frictional impulse= μJ = 3μmv/2
therefore velocity is v/2(given in perpendicular direction) and μ3v/2 in tangential direction.
Torque due to frictional impulse = μJR = 3μmvR/2
3μmvR/2=2/5mR2(ω+ω0).. say final ω is in direction opposite to initial..
ω=(15μv/4R)-ω0... in opposite sense as initial ω...
◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘
Q.4)
◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘
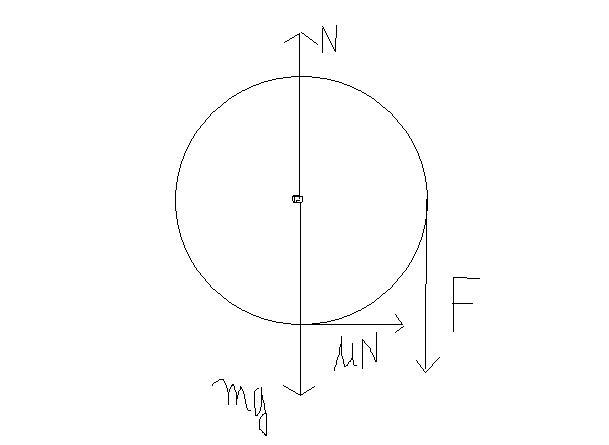
N=(mg+F)
μN=ma...... a=αR
μ(mg+F)=mαR ...(i)
(F-μN)R=mR2/2α
(F-μmg-μF)=m/2(αR).... (ii)
From (i) and (ii)
(F-μmg-μF)=(μmg+μF)/2
F=(3μmg)/(2-3μ)....
◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘◙◘
hmmm.... amazingly whats special about μ=2/3.... [12]
43) mu=1/2. n friction=4.48N ????????????
and acceleration of M = 7X1.12/5 ????????????????
Ans given for 43 are 3.75m/s2, 12N and ang accn of cylinder = 30rad/s2 (clockwise)
(m/Ï€iR2)2Ï€xdx is mass of ring...
and μdmgx = torque... (x is distance of that ring.)
please solve it. i am not able to properly write the torque eqn.
Q.52..
part a) is hint for part b)
Notice that no force acts on rod in horizontal direction (as surface is smooth..)so acom in horizontal direction is 0. initially vcom =0 in horizontal direction so it(COM) will fall in straight line...
for part b)
ωlcosθ = vcom
2
mgl/2-mgl/2(sinθ)=1/2mvcom2+(1/2)(ml2/12)ω2
solve it to get the answer..
hmm... post whatever u have done in that.. it would be more beneficial...
For Q. 52 if its not clear..
see: http://targetiit.com/iit_jee_forum/posts/fjee_aits_rotation_2052.html
areyyyyyyyyyy!!! mereko yeh q.1 ka case abhi samajh me aya ...!!
lol!
i have been thnking from day1 ki the disc is vertical ...
figure hi nahi chamka ...
aaj chamka!
[3] [3]
and abhiisekh, u drew it in such a way as if it is vertical...
and i had bn thinking from that day... yeh kaisa question hai! vertically ghoomra aur friction flat portion pe act karra!
hey gv fig along wid questions re!
http://www.goiit.com/upload/2009/2/2/05bc183d08fe220370c490fde69d3e22_70619.png
man koi itna question ek topic ka kaise bana sakta hai... all same ones.. i solved only first one .. :P
Q3. A perfectly rough inelastic sphere of radius a is rolling with velocity v on a horizontal plane when it meets a fixed obstacle of height h. Show that if a√70gh/(7a-5h)<v<7a√(a-h)g/(7a-5h) then the sphere will overcome the obstacle.
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F. Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k.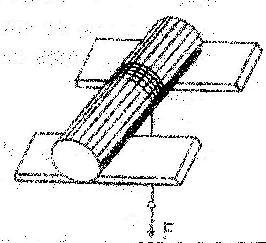
Q2. A rotating ball hits a rough horizontal plane with a vertical velocity v and angular velocity ω. Given that the coefficient of friction is μ and the vertical velocity of the ball after the collision is v/2, find the angular velocity after collision.
A disc rolls upon a straight line on a horizontal table, the flat surface of the disc being in contact with the table. If be the velocity of the center of the disc at , find the time after which the disc comes to rest. Given the coefficient of friction between the disc and the table is: