1is the linear acceleration of cylinder =3F3M+m
A plank of mass 'M' is placed on a smooth surface and a cylinder of mass 'm' and radius 'R' placed over the plank. now there is a horizontal force 'F' acting on the plank towards right. if the cylinder does not slip over the surface of the plank find linear acceleration of the plank and the cylinder. and also find the angular acceleration of the cylinder.
please solve it without using pseudo force.
-
UP 0 DOWN 0 1 4
4 Answers
1
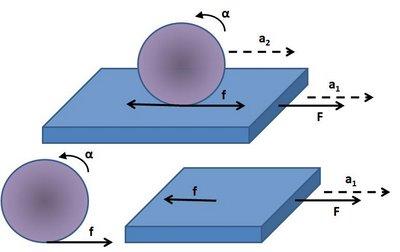
im just having problem with the constraint relation.
R * α = ?
pls explain this part. im really bad at constraints.
we get the answer with this equation,
R * α = a1 - a2 ..
but then my doubt is suppose a1 < a2 => relative acceleration of the cylinder is negative that is opp. to dir. of acc. of plank..
but it shud be positive na as if a1 < a2 cylinder is more accelerated than the plank
1
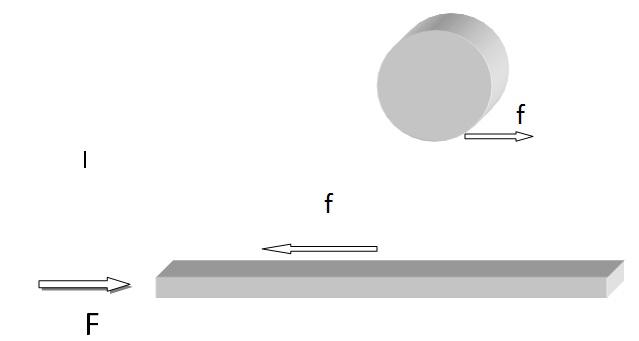
F-f=Ma_{p} \\ f*R=I\alpha \\ f=ma_c \\ a_c+R\alpha=a_p ...{\texttt{For Pure Rolling}}\\ \texttt{From that we get } \\ f=\frac{F}{\frac{3M}{m}+1} \\ \texttt{We get }a_p \ as \\ a_p=\frac{3F}{3M+m} \\ \alpha=\frac{2F}{R(3M+m)}