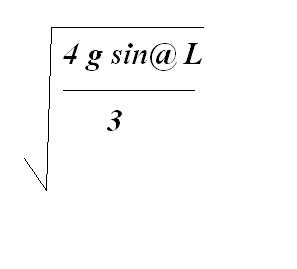1
1try it out guyz...its definitely worth a try...
 1
1the final velocity of disc down the plane will be 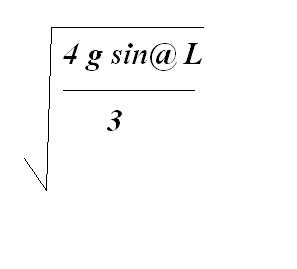
where L is the length of incline.
(ans. i gave is assuming that the disc starts from top with zero velocityand reaches down with velocity i mentioned)
 3
3assuming incline is fixed ........
now if its inelastic collision vsin@ will remain along incline
now let coeff of friction be ' u ' [ assuming vsin@>WR]
2ugcos@/R = A[alpha]
-ugcos@ = a .............
let after time t they attain pure rollin
vsin@ - ugcos@t = WR + 2ugcos@t
[vsin@ - WR]/3ugcos@ = t
vsin@ - vsin@/3 - WR/3 = vf
vfinal = 2vsin@/3 - WR/3 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
hope thats the answer
 1
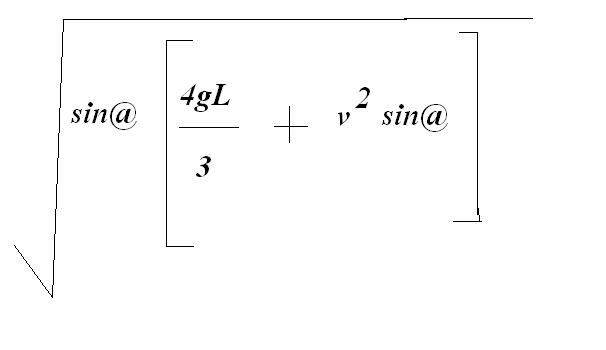
1assuming inelstic collision
final velocity is
 1
1L is length of incline and velocity i wrote is the final velocity when disc reaches down the plane.
(hope u r talking about that final velocity only)
 3
3i think he wants the velocity after it starts pure rolling that is the final velocity of the disc .....i dont think we req. length of inclined plane pa ...
 1
1dudes i mite probably have been not clear to u...sayi make it more clear..assume dat at d very instant it hits d plane, tstarts pure rollin...iitcoming, uve assumed d normal force to be mgcos@...which is not correct at the instant it hits d plane...after words it becomes mgcos@....when it hits the plane theres an impulsive normal force, and dus an impulsive frictional force...try it...
 1
1guyz?? no takers?? i know all of u can crack dis down...
 1
1any one, jus kill it...i know u can...
 1
1dudes please try it....its worth a try urself...ill give tym till tonite...asish,iitcoming, others, please give ur try...
cheers!!!
 3
3mvsin@ = J ..........
uJdt = frictional force(initial neglecting mgcos@)........
umvsin@R= (mr^2/2)(W1-W)
thus we can find final W1
final v = uvcos@ + vsin@
now this stuff is not pure rolling ...... it will take sum time ................:P
so vfinal - ugcos@t = W1R + 2ugcos@t
solving for t .......... and putting value of t.. we get v final....
 1
1Okay...
the question says that what is the final velocity if the cylinder falls on the plane and starts pure rolling...iitcoming, does ur answer contain 'u'(coeff of friction)...the question says that the friction is enuff to make the cylinder pure...
anyways, there are 2 methods,
1) assume that the disc experiences a large normal force, N for a short time 'dt'
let the final velocity be V
we have
m(vsin@-V)=KNdt---1)
also that
mR2/2((V/R)-w)=(KNdt)R---2)
V comes out to be
(2vsin@+wR)/3
and w final = V/R
the second method is by "conservation of angular momentum about the point of impact"
that is
L initial=Lfinal
or
mwR/2 + mvRsin@ =3/2mVR
or
V=(2vsin@+wR)/3
again final w=V/R
cheers!!!
 3
3no... it gets cancelled out ............................
yaar ... is it given that immidiatly after collision it starts pure rolling???????????????????? i did the same thing u did in ur first method and i didnt assume it already startted pure rolling and i gave its sum time to pure roll !!!! :P ......... its nowhere in ur question that it instantaneously starts pure rollin