2g5
 Sourish Ghosh Sir, what will be the answer to this question?Upvote·0· Reply ·2014-05-09 21:27:14
Sourish Ghosh Sir, what will be the answer to this question?Upvote·0· Reply ·2014-05-09 21:27:14 Akash Anand I am getting 2g/3. I guess ..may be you have made some mistake in constraint relation part.
Akash Anand I am getting 2g/3. I guess ..may be you have made some mistake in constraint relation part.
A cylindrical pulley of mass M and radius R is connected to another pulley of mass M/2 ,R/2 through a massless string as shown. If sufficient string is wrapped over larger pulley,find the accleration of mass M attached to the smaller pulley when whole system is released from rest .(assume there is no slipping in the smaller pulley)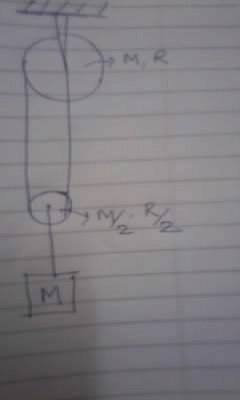
2g5
Sir,for the first constraint velocity of the string near the bigger pulley and near the smaller pulley must be same.
therefore,
α1R=α2R/2 + a
and the second one is α2R/2=a
solving these two equations
α1R=2a and α2R=2a.
where am i going wrong?
the correct answer is 2g/5. In AAKASH ANAND'S solution the first constraint relation is wrong. Instead of \alpha_1R=\frac{a}{2}, it must be \alpha_1R=2a. Rest of the equations are correct. This change will give the correct answer. that is \frac{2g}{5}.
