A uniform cylindrical pulley of mass M and radius R can freely rotate about the horizontal axis O. The free end of a thread tightly wound on the pulley carries a dead weight A. At a certain angle α it counter balances a point mass m fixed at the rim of the pulley. Find the angular frequency of small oscillations of the arrangement (refer figure).
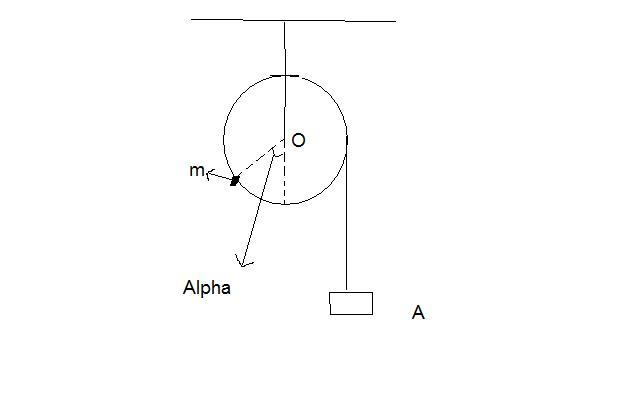
Attempt-
Let the mass of the dead weight be m1
Considering rotational equilibrium about O, we have
m1gR = mgRsinα
i.e. m1 = msinα
Let the pulley be displaced through a small angle ∂ in the clockwise direction.
The Total Energy of the system after rotation through the small angle is-
E = mgRcos(α + ∂) - m1gR(α + ∂) + Iω²/2 + m1ω²R²/2
As the system is conservative, the time derivative of energy is 0
dE/dt = 0
on solving the above equation,
I got dω/dt = mgRsinα + m1gR/(I + m1R2)
Now m1 = msinα and I = MR²/2 + mR² ( I did not include m1R² as I already took its kinetic energy as m1ω²R²/2)
on solving further,
dω/dt = 2mgsinα/[(1+sinα)mR +MR/2]
which is not proportional to ∂!!!
and hence not a S.H.M.
The answer given is ω² = 2mgcosα/[MR + 2mR(1+sinα)]
Please help!!
-
UP 0 DOWN 0 0 3
3 Answers
1Sorry guys....I forgot to add the figure......plz tell my mistake and solve it....
23i m getting exact answer
suppose mass of block = m1 ,
we hav m1 = msinα
let the pulley rotate clockwise by small θ
and let the resultant angular accn = β
Wgravity = ΔKE
m1grθ + mgr ( cos (α+θ) - cosα) = 12m1r2ω2+12mR2ω2 + 14MR2ω2
differentiate both sides wrt time
m1grω - mgrsin(α+θ)ω = 122m1r2ω(β)+122mR2ω(β)+ 142Mr2ω(β)
i.e
[ m1 - msin(α+θ) ]g= β2 (2m1r +2mr +Mr )
m1 - msin(α+θ) = msinα - m (sinαcosθ +cosαsinθ)
as θ is small , cosθ ≈ 1 , sinθ≈θ
so,
g[ m1 - msin(α+θ)] = - (mgcosα)θ = β2 (2mr(1+sinα) +Mr )
now u can find angular frequency
actually using torque ,this question is very easy
mgRsin(α + θ) - m1gR = β Σ I
i.e
mgR(sinαcosθ+cosαsinθ - sinα ) ≈ (mgRcosα)θ = β Σ I
energy method shud be used only when writing torque/force equations is difficult
1Thanks alot for your reply
why does this expression become 0 on expanding cos(α+θ) before?
m1grθ + mgr ( cos (α+θ) - cosα)
mrgθsinα + mrg( cosα - θsinα - cosα) =0???