3First i will rite an energy equation for a small oscillation for the whole system and then diff it to get the 'w'
find freq. of small ossilations ...............everythin else prov. in figure!!!!
-
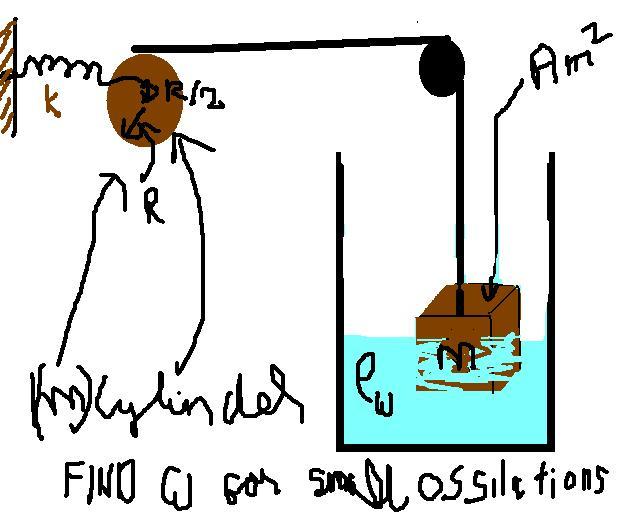
UP 0 DOWN 0 0 16
16 Answers
3
3this is the best question ive ever found in SHM .... and the sense of satisfaction u get after solvin it is immense!!!!![1][1][1][1][1][1][1]
3all physics lovers [3] also see the question of the day forum!!!!!!
1exactly wo solid ke barre mein kya lika hai
kahi ye density to nahi hai
1we'll ablnce d torues let d small displcmnt b x so let d tension b T so TR-kxR/2=Ialpha and T+l^2xÏ=mg yeh dohno solve karke woh x ke terms emin gadbad ho ri hai :(
here i assumed l as lenght of d cube
3its the distance of the spring from the center of the cylinder .... A is the area of crossection........ get ans. in terms of watever is given only!!!!!
HINT its only ΔT that matters !!!!!!
24ok......iit..........give some more time..........i couldnt understand the fig..........now i will try.....[1][1]
3okie now as i gave in my hint we will concider ΔT only!!!!!!!!!!
now let us take the block to be pushed in by distance x................
an extra ÏgAx acts upward and also theres an accn. say a upward !!!!!!!!!!
so ΔT + ÏgAx =ma.........
ΔT = ma - ÏgAx ........
x = Rθ if the cylinder is displaced by an angle θ
................
now comin to the spring .........
if the disp. of the cylinder is θ ......
the extension in spring is R/2θ .......
so Fsp = kR/2θ .............
now coming to torques acting on the cylinder......
kR/2θ(R/2) - ΔTR = (MR2/2)(ω2θ)
kRθ/4 - ma + ÏgARθ = (mR/2)(ω2θ)
kRθ/4 - mω2(Rθ) + ÏgARθ = mR/2(ω2θ)
k/4 + ÏgA = 3/2 m(ω2 )......
k+4ÏgA /6m = ω2 ...
√k+4ÏgA /6m = ω .............
if u guys hav simpler methods do post!!!!![1]