33yup..
T has to remain same... and thers no problem in slipping.. :)
33 Answers
33
33that segment m=0 is any segment of rope...
if rope is same tension will be same throughout the rope for massless and friction condition
106but priyam in the question, if the extensions in the springs will not be equal, then the system will become tilted. thats y im thinking that extensions in both springs will be same......
33tilt kaise hoga... pulley ghum jaega... i was fool.. :P
thread will slip over pulley.. ...edited..
33
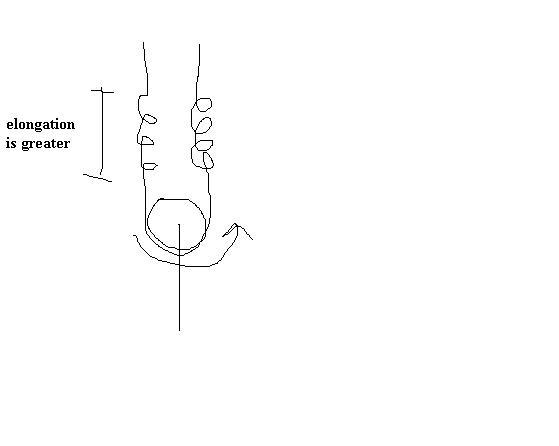
here pulley is not rotating just thread slipping over it...as pointed by Ashish in below post.. :)
106lekin pulley to frictionless hai naa, to phir ghuumega kaise?
106thread can slip but tension has to remain the same.... is that right?
62arrey mujhe laga tha that was ur post... (Din see it was sky's :)
3simple 1........
if u displace block bt x then springs will get displaced by 2x......................
so net tension = T...................
T = 6k(w)....T/2=3kw.......
T=3Kj..............
3/2T=3K(w+j)....w+j=2x...........
T=4kx......
but 2T ACTS ON BODY!!!!!!!!!
2T=8kx.......................
mw^2x = 8kx ........
w=√8k/m..........
39the two springs are in series. so effective spring constant is 9k. therefore answer is a ...............
106priyam : why tension is same in both threads? i might be asking silly questions but still please answer it..
33Let x1 and x2 be elongation in 3K and 6K springs
now since tension in thread is same above pulley so 6Kx2=3Kx1
x1=2x2=T
Now work done by tension is zero.. so
Tx1+Tx2=2Tx.... where x is displacement of block...
solving these eqns we get..
x1=4x/3
so T=3Kx1=4Kx
but force on block is... 2T or 8kx=ma so ω=√8k/m
Why i have neglected gravity... [4]
1well forgot to tell.. Fr = restoring force... [hope this is understood .. but still ]
106sky y have u done Fr/k1 btw Fr/k1 has unit meter^2 where as LHS has unit meter.
12x = Fr/K1 + Fr/K2
=> x = Fr [1/k1 + 1/k2 ] /2
but 2Fr =mw2r [y?[1]]
so, x = 2Fr [1/k1 + 1/k2 ]/4
=> x = mw2x [1/k1 + 1/k2 ] /4
=> w2 = 4k1k2/(k1+k2)/m
here, k1=6k, k2=3k , m=m :P ,
so, w2 = 8k/m [1]
33interesting...
both type of combi in above posts..
seires by mathe.. parallel by rkrish..