3of u want to know how its suspended luk at figure!!!!
a massive circular hoop of radius r ossilates in its own plane about a horizontal axis at a distance x above the centre of the hoop the period of oscillation is minimum when x equals
Please explain how it is suspended
-
UP 0 DOWN 0 0 9
9 Answers
3okie so basically its a ring na.........
so for HORIZONTAL axis thru center its 1/2mR2 .......
at distance x from center its 1/2mR2 + mx2 ..................
mgxθ = (1/2mR2 + mx2)ω2θ ...............
gx/(1/2R2 + x2 ) = ω2 ......
differentiate wrt to x and for maxima condition(of omega and minima for period)
dω/dx =0 ..
g(1/2R2 + x2) = gx(2x) ......
1/2R2 = x2
x = R/√2 ..!!!!!!!!!!
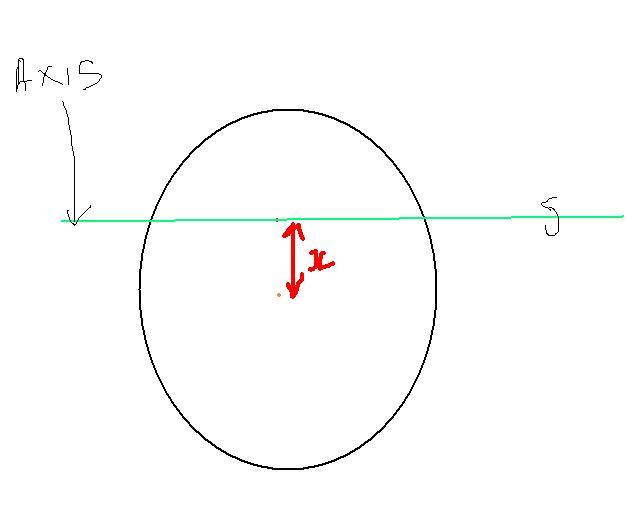
3NO ITS HORIZONTAL AXIS KARAN ....APPLY PERPENDICULAR AXIS THEORM!!!!!!!![1] .. ITS SURELY MR^2/2
62yes karan.. it is not perpendicular to the plane.. it is passing through the diameter..
so the I is as given by iitimcoming.
1If according to you we take axis in the plane of the ring then how can the ring rotate in its own plane Thus axis has to be perpendicular to the plane and also it is horizontal and also the ring will rotate in its own plane If we take the axis as i am saying then i am getting the ans as x=R There is no option in the test as R/√2
3"""""ossilates in its own plane about a horizontal axis """""""" y cant it rotate in its own plane [3] ..........may be theres a mistake in the options!!!!!
1I think this is a ques from the topic compound pendulum
Moreover it is suspended from a point Therefore how can it rotate